Tests de comparaison des valeurs mesurées
Il arrive très souvent que lors d'un mesurage d'un paramètre que l'on réitère plusieurs fois, une des valeurs n'est pas représentative des autres, que faire?
- Ecarter la valeur arbitrairement mais c'est peut-être la seule valeur qui soit représentative du paramètre,
- Refaire d'autres mesurages pour augmenter le nombre de valeurs (surement la meilleure réponse mais en avons-nous le temps?),
Les tests statistiques peuvent parfois répondre à nos questions, j'attire l'attention sur le fait que ces tests ne permettent pas de résoudre tous les problèmes cas on part de l'hypothèse que le peu de valeurs disponibles suivent une loi normale (ce qui n'est peut-être pas le cas) mais ils ont l'avantage de clarifier les choses et d'obtenir la même conclusion quel que soit l'opérateur qui réalise les mesurages et c'est déjà pas mal.
En fait, cela dépend de la complexité de la mesure, si c'est rapide, on peut refaire quelques mesurages, et on prendra la moyenne de toutes les valeurs obtenues mais s'il s'agit d'essais destructifs couteux que l'on ne peut pas refaire à son gré, il faudra bien prendre une décision.
On va utiliser des tests pour éliminer les valeurs aberrantes:
Considérons un opérateur qui réalise un contrôle qualité, son protocole lui impose de vérifier la teneur en sucre d'un sirop, le nombre de mesure n'est pas spécifié et comme notre opérateur à une conscience professionnelle, il réalise systématiquement 3 dosages et note la moyenne obtenue sur une carte de contrôle qui est bornée par un maxi et un mini.
Notre opérateur ne dispose pas de critère pour estimer si les 3 mesurages sont équivalent et lorsque, une des valeurs n'est pas identique au 2 autres et que de surcroit, cette valeurs sort légèrement des tolérances imposées, il se sent mal à l'aise, il tâtonne: moyenne sur les 3, n'en prendre que 2?
Prenons les 3 valeurs (X
| 30,5 |
30,1 |
32,6 |
La tolérance en sucre est de 30,0±1,5 g/L
![]()
Test N°1: Test de GRUBBS
On calcule la moyenne des 3 résultats: x̄=31,06 g/L
On calcule l'écart-type s de la série de donnée: s=1,343 g/L
La valeur la plus éloignée de la moyenne est la N° 3: X
On va calculer la valeur de GRUBBS avec la relation suivante:
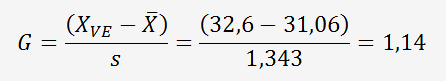
Avec une Probabilité de 95 %, G pour 3 valeurs doit être < 1,155 (table de GRUBBS) voir ci-dessous
On ne peut pas éliminer la valeur "aberrante".
![]()
Test N°2: Test de DIXON (≤25 valeurs)
On doit mettre dans un premier temps, les valeurs dans l'ordre croissant:
| 30,1 |
30,5 |
32,6 |
avec X
On calcule le τ
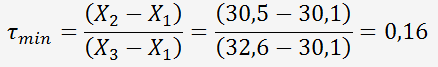
On calcule le τ
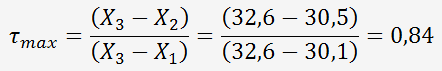
Puis on calcule le τ
![]()
Avec une Probabilité de 95 %, τ
On ne peut pas éliminer la valeur "aberrante".
![]()
Test N°3: Test de CHAUVENET
On calcule la moyenne des 3 résultats:x̄=31,06 g/L
On calcule l'écart-type s de la série de donnée: s=1,343 g/L
On va déterminer le d
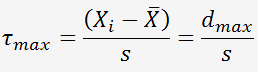
La probabilité d'obtenir une valeur qui s'écarte
de plus de d
![]()
Les probabilités en fonction du nombre de valeurs (x 3) sont données dans le tableau ci-dessous:
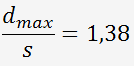
On peut donc calculer d
et par conséquent X
![]()
Test N°4: Test de THOMPSON modifié
Il ne fonctionne qu'avec 4 valeurs au minimum:
| 30,1 |
30,5 |
30,3 | 32,6 |
On calcule la moyenne des 4 résultats:x̄=30,87 g/L
On calcule l'écart-type s de la série de donnée: s=1,16 g/L
On va déterminer δ qui doit répondre à l'inégalité suivante:
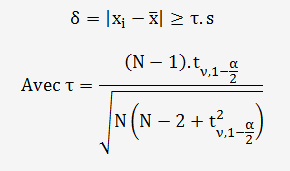
Exemple pour N = 4 et α = 0,05 en sachant que ν = N-2:
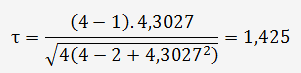
Vous pourrez retrouver les valeurs de Alpha dans la fiche: les intervalles de confiance
Nous avons donc δ = l32,6-30,87l=1,73 ≥ 1,425.1,16=1,653, la valeur de 32,6 peut être considérée comme aberrante et écartée de la série.
Les autres tests nécessitent plus de valeurs individuelles.
Les valeurs de Test sont donnés pour une probabilité de 95%
| N |
Critère
de Chauvenet |
Test
de Grubbs |
Test de DIXON | Critère de Thompson |
| 3 |
1,38 | 1,155 | 0,970 | 1,1511 |
| 4 |
1,54 | 1,481 | 0,829 | 1,4250 |
| 5 | 1,65 | 1,715 | 0,710 | 1,5712 |
| 6 | 1,73 | 1,887 | 0,625 | 1,6563 |
| 7 | 1,80 | 2,020 | 0,568 | 1,7110 |
| 8 | 1,87 | 2,126 | 0,526 | 1,7491 |
| 9 | 1,91 | 2,215 | 0,493 | 1,7770 |
| 10 | 1,96 | 2,290 | 0,466 | 1,7984 |
