Exemple de propagation des erreurs
La loi de propagation des erreurs est très utile si par exemple, vous avez l'obligation par manque de moyens d'utiliser un même équipement pour mesurer des dimensions différentes sur un même objet et utilisées pour déterminer une surface.
Degré de liberté
C'est souvent une estimation qui est oubliée dans la détermination de l'incertitude, pourtant, le facteur d'élargissement peut modifier de manière significative l'incertitude finale.
LE GUM
- Modélisation du processus de mesure (consiste à écrire
sous forme mathématique la façon dont sont utilisées toutes les informations
qui sont à la disposition de l’expérimentateur), ce qui peut être difficile
ou impossible;
- Estimation de l’incertitude de mesure (grandeur de sortie) à partir
des incertitudes des grandeurs d’entrée;
- Besoin de connaître toutes les sources d’erreurs possibles (grandeurs
d’influence, étalonnage, erreurs de lecture…);
- Difficile cependant à mettre en œuvre dans le cas d’essais complexes.
Analyse du processus de mesure afin de déterminer une
relation mathématique réunissant toutes les informations dont dispose
l’utilisateur:
Y (mesurande) = f(X1, X2, ……Xn)
- Identification des composantes des sources de causes d’erreurs.
- Estimation des incertitudes type pour chacune des sources individuelles contribuant a l’incertitude du résultat, sur chaque grandeur d’entrée.
- Détermination de l’incertitude type composée (loi de propagation des incertitudes).
- Détermination de l’incertitude élargie et présentation du résultat de mesure.
Le recensement des erreurs est réalisé avec la méthode des 5 M qui analyse le processus de mesure afin de lister toutes les composantes liées à l’incertitude du résultat.
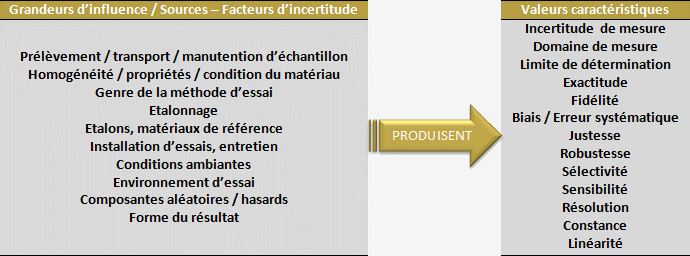
Chaque composante de l’incertitude est évaluée statistiquement séparément (Type A ou B);
L’incertitude composée est ensuite calculée par combinaison des incertitudes selon la loi de propagation, c.-à-d. en fonction de la formule mathématique (f) de calcul du résultat.
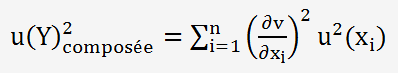
L’incertitude composée U(y) est la racine carrée de la somme des dérivées partielles au carré (corrélations exclues).
Quelques formules bien pratiques pour déterminer les dérivées partielles.
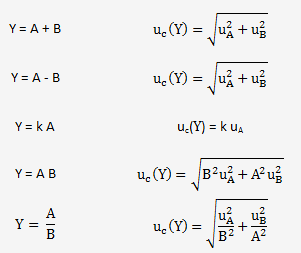
La composition quadratique des contributions individuelles (qui est par ailleurs caractéristique de la théorie classique de composition des erreurs) tient compte du fait que la probabilité que toutes les composantes constitutives assument simultanément leur valeur maximale et qu’elles soient du même signe est très faible.
La moyenne quadratique repose sur le théorème de Pythagore:
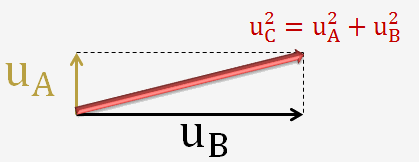
Ceci n’empêche que dans certains cas, des approches conservatives avec somme numérique de toutes ou certaines composantes peuvent être adoptées.
On note qu’une telle estimation peut s’avérer très approximative dans le cas où l’essai ne consiste pas à une séquence directe d’opérations caractérisées par les contributions Ui (comme par ex. dans le cas d’une série de pesées ou mesures de volume couplées avec des lectures d’instruments) mais au résultat final, on arrive à une seule opération ou un ensemble d’opérations simultanées dans le cadre desquelles différentes sources d’incertitude agissent simultanément.
Dans ce cas, en effet, il n’est pas dit que les simples composantes d’incertitude se transfèrent « directement » sur le résultat final, mais elles peuvent être atténuées ou amplifiées.
Les laboratoires de Biologie médicale pourront se consulter le guide du COFRAC: SH GTA 14.
Remarque: les dérivées partielles sont appelées coefficients de sensibilité.
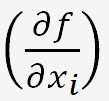
Il est pratiquement impossible d’évaluer individuellement l'effet de chaque grandeur d'influence sur l'incertitude.
De plus, l’expérience a montré que les incertitudes issues de la méthode analytique-mathématique sont le plus souvent plus faibles.
Lorsqu'il est question de méthodes bien décrites dans des normes ou
des documents normatifs dont les valeurs caractéristiques de base sont
connues.
La validation de la procédure est considérée comme ayant été concrétisée
par le travail de "normalisation".
Il faudra cependant démontrer:
1. le suivi scrupuleux de la norme et son instruction;
2. la connaissance et la maîtrise des grandeurs d’influence;
3. La possibilité à la demande d’un client de fournir une incertitude cohérente sur le résultat.
- principalement des essais de répétabilité (avec matériaux de référence),
- également des essais de reproductibilité,
- et, afin de démontrer la bonne maîtrise de l'essai, des comparaisons directes entre résultats.
Il convient, outre la procédure d’essai complète, de documenter:
L'incertitude type globale ou composée sera en principe donnée sous forme élargie (k=2 - attention, ce n'est pas toujours le cas), et devra clairement mentionner:
- qu’elle correspond à une distribution normale supposée à un niveau de confiance d’environ 95%,
Ceci signifie que, dans 95 % des cas, l’écart entre la valeur inconnue (x) du résultat final d’un essai ou analyse (ou la valeur inconnue du mesurant) et la valeur moyenne (xm) des résultats d’essai ou analyse obtenue (ou la valeur moyenne des résultats des mesures effectuées) ne dépasse pas l’intervalle d’incertitude spécifiée U.
- les grandeurs d'influence significatives éventuellement exclues, p. ex. l'échantillonnage.
Dans certains cas, il peut être nécessaire d’introduire des précautions particulières en adoptant une valeur de k égale à 3 qui corespond à un intervalle de confiance égal à environ 99 %.
Il y a donc une très faible probabilité que l’erreur commise soit supérieure aux limites correspondant à cette valeur d’incertitude.
Lorsque les données sont indépendantes (non-corrélées), on peut utiliser l’équation de type:
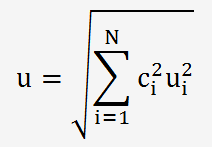
Mais lorsque l’incertitude d'un paramètre est corrélée avec celle d'un autre paramètre (par exemple: des dimensions qui sont mesurées simultanément avec le même pied à coulisse).
Il faut utiliser la formule suivante (propagation des incertitudes):
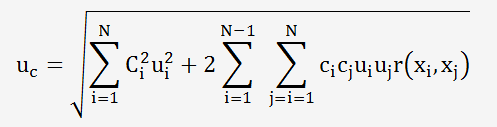
Le coefficient r(xi,xj) caractérise le degrés de corrélation entre les données:
Pour des données non corrélées, r = 0
Pour des données parfaitement corrélées, r =-1 ou +1
Pour des données plus ou moins corrélées, r varie entre -1 et +1
Pour estimer ce coefficient de corrélation, il faut estimer la covariance entre les données.
Elle est estimée par la formule suivante:
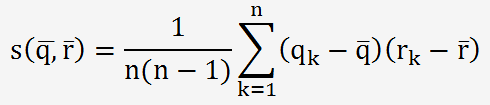
Le coefficient de corrélation est donné par le rapport:
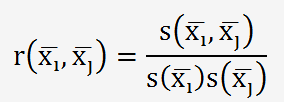
Il se peut que Uc(y) ne soit pas fiable si parmi les incertitudes types prépondérantes qui ont servi à son calcul, on en trouve qui proviennent:
- d’un petit échantillon
- d’une estimation personnelle raisonnable.
- d'une moyenne qui repose sur des valeurs différentes et dont l''impact à une influence directe sur le résultat.
Pour quantifier la "fiabilité de uc(y) on calcule le nombre de degrés de liberté effectif avec la relation de Welch-Satterthwaite:
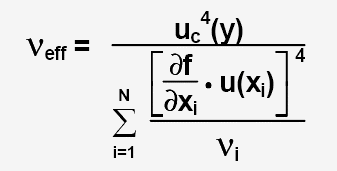
La valeur de Uc(y) est d’autant plus «fiable» que Veff est élevé.
Pour les incertitudes de type A, le degré de liberté est égale au nombres d'essais - 1 (n-1).
Si l'incertitude est réalisée à partir d'une régréssion linéaire, le degré de liberté vaut (n-2).
