Définition de la règle de décision:
Règle documentée qui décrit comment l'incertitude de
mesure sera comptabilisée en ce qui concerne l'acceptation ou le rejet
d'un élément/objet, compte tenu d'une exigence spécifiée
et du résultat d'une mesure.
Cette prise de décision peut être lourde de conséquence, pour le laboratoire d'une part qui prend le risque de déclarer un produit conforme alors qu'il ne l'est pas et pour le client qui risque de refuser un produit non conforme alors qu'il ne l'est pas.
En tout état de cause, les informations fournies en rapportant le résultat de l’essai et son incertitude doivent être liés aux exigences du client, aux spécifications et à l'utilisation prévue du résultat.
Si le risque est grand et que la déclaration de la conformité est très limite, l'échantillonnage devra obligatoirement être étendu pour diminuer le risque et affiner le résultat moyen lorsque cela est possible (disponibilité des échantillons, possibilité de réitérer les résultats).
Dans des cas exceptionnels où des facteurs particuliers peuvent influencer les résultats, mais où l’étendue ne peut être mesurée ou raisonnablement évaluée, la déclaration doit inclure la référence à ce fait.
Toute incertitude résultant du prélèvement, n'étant pas entièrement représentatif du produit, devrait normalement être identifiée séparément dans l'évaluation de l'incertitude.
Cependant, si il peut ne pas y avoir d'informations suffisantes à cet effet, dans ce cas, une déclaration possible pourrait être : « Les résultats d'essais de ce rapport concernent seulement l'échantillon soumis à l'essai et non pas le produit sur lequel l'échantillon d'essai a été prélevé ».
Rappelons certains principes de base qui malheureusement vont démontrer que même dans des cas favorables, nos équipements et nos essais ne nous apportent pas toute la confiance que l'on souhaiterait en regard de la tolérance imposée par une spécification.
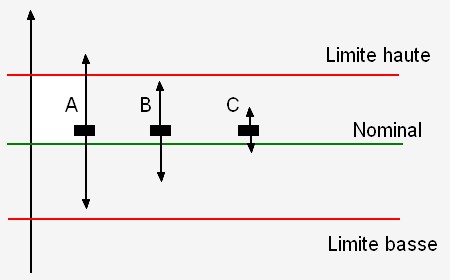
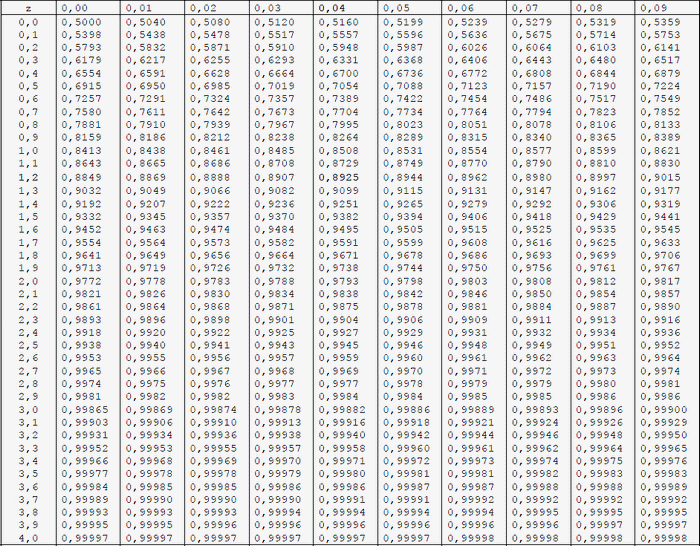
Si l'on considère 3 résultats identiques ayant chacun une incertitude
propre fournie avec une probabilité de 95%, on remarque que le résultat
A avec son incertitude U
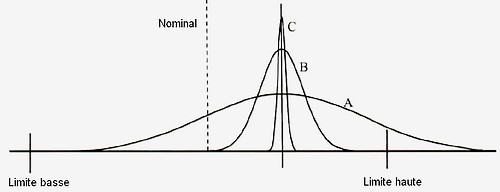
En considérant que le laboratoire C à une incertitude élargie
U
Déterminons le TUR (Test du taux d'incertitude), il est déterminé par la relation suivante:
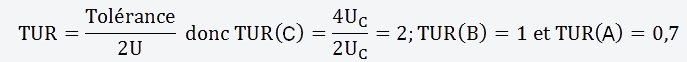
Cette règle simpliste généralement appliquée est le 4 pour 1, on remarque que pour ces cas de figure, nous n'avons pas un résultat ≥4, l'incertitude est trop importante en regard de la tolérance, ce qui sera malheureusement régulièrement le cas, cette méthode ne définit aucun risque, elle permet juste de se faire une idée de la proportion de l'incertitude de mesure par rapport à la tolérance.
Afin de décider si oui ou non accepter / refuser un produit, étant
donné un résultat et l'incertitude, il devrait y avoir:
a) une spécification donnant les limites supérieures et / ou
inférieures autorisées des caractéristiques (mesurandes)
contrôlées et
b) une règle de décision qui décrit comment l'incertitude
de mesure sera prise en compte en ce qui concerne l'acceptation ou le rejet
d'un produit selon sa spécification et le résultat d'une mesure.
c) La règle de décision devrait comporter une méthode
bien documentée pour déterminer sans ambiguïté l'emplacement
des zones d'acceptation et de rejet, idéalement en indiquant ou en
utilisant le niveau minimal acceptable de la probabilité que le mesurande
se situe dans les limites de spécification.
On devrait également fournir des instructions pour traiter les mesures répétées et les valeurs aberrantes lorsque cela est possible.
d) En utilisant la règle de décision, la taille de la zone d'acceptation ou de rejet peut être déterminée au moyen de bandes de garde appropriées.
La taille de la bande de garde est calculée à partir de la
valeur de l'incertitude de mesure et du niveau minimum acceptable de la probabilité
pour que le mesurande se situe dans les limites de spécification.
e) De plus, une référence aux règles de décision
utilisées devrait être incluse dans les rapports sur la conformité.
En contrôle de conformité, la valeur mesurée
est comparée à une ou deux limites d'acceptation (borne maxi
ou mini uniquement ou tolérance).
Si la valeur mesurée est dans la zone d'acceptation, le produit est
considéré comme conforme, s'il est en dehors de la zone d'acceptation,
le produit est considéré comme non conforme et sera rejeté.
Les limites d'acceptation peuvent être des limites de spécification technique ou des limites de contrôle plus strictes.
En raison de l'incertitude de mesure, le résultat
de mesure y et la valeur réelle de la caractéristique observée
x diffèrent l'un de l'autre.
La décision sur la conformité d'un produit basée sur
y = x + U: valeur mesurée comme la somme de la valeur réelle
et de l'incertitude de mesure U mais la conformité du produit est influencée
par la relation entre la valeur réelle x et la valeur supérieure
(LSS) et la limite de spécification inférieure (LSI).
Cette tolérance peut fournir quatre résultats différents
sur la prise de décision: acceptation formelle, rejet direct et deux
types d'erreurs sur la prise de décision.
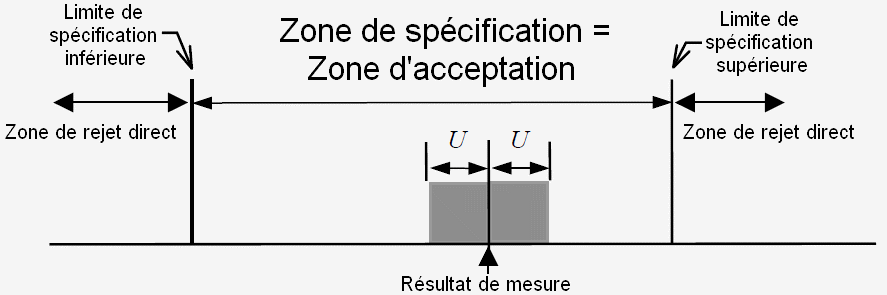
La règle de décision, présente des difficultés proches des limites de la zone de spécification.
En raison de l'incertitude de mesure, un produit avec un résultat de mesure juste à l'intérieur de la limite de spécification peut effectivement être non conforme et a fortiori juste à l'extérieur de la zone de spécification.
Si les pièces non conformes ont un impact économique important, il est préférable de mettre en place une bande de garde bilatérale.
La bande de garde est une technique qui dans un sens peut
produire une zone d'acceptation réduite (plus petite que la zone de
spécification) en raison des bandes de garde.
La largeur de la bande de garde: g, est exprimée en
pourcentage de l'incertitude étendue, par ex. une bande de garde de
100% à une amplitude égale à l'incertitude élargie.
L'établissement de l'amplitude d'une bande de garde est une décision entre l'OEC et le client et repose sur des considérations économiques, tandis que l'évaluation de l'incertitude de mesure, U, est une activité technique qui dépend du processus de mesure.
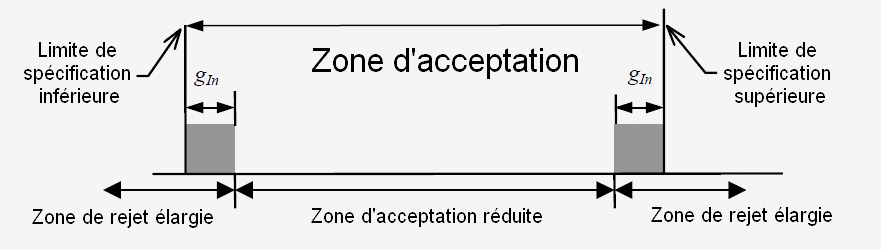
Dans cette configuration, une zone d'acceptation réduite implique à la fois une diminution de la largeur de la zone d'acceptation et une augmentation de la confiance qu'un résultat de mesure dans cette zone soit associé à un produit conforme aux spécifications.
Dans ce cas de figure, la probabilité que l'OEC obtienne des résultats conformes est réduite mais la probabilité que le client s'assure que ses pièces soient bonnes est augmentée (avec le risque de se voir refuser un lot).

La situation inverse peut également s'appliquer, la zone d'acceptation est élargie et prend en compte la bande de garde bilatérale pour la déclaration de la conformité.
Dans ce second cas de figure, la probabilité que l'OEC obtienne des résultats conformes est élargie mais la probabilité que le client s'assure que ses pièces soient toutes bonnes est réduite.
La taille de la bande de garde g dépend de la valeur de l'incertitude et est choisie pour répondre aux exigences de la règle de décision.
Par exemple, si la règle de décision indique que pour une déclaration
de produit non-conforme, la valeur mesurée doit être supérieure
à la limite + U, alors la taille de la bande de garde est 2u.
Si la règle de décision indique que pour une déclaration
de produit non-conforme, la probabilité P que la valeur du mesurande
soit supérieure à la limite LSI, devrait être d'au moins
95%, alors g doit être choisi de sorte que pour une valeur observée
de LSI + g, le probabilité que la valeur du mesurande se situe au-dessus
de la limite LSI est de 95%.
De même, si la règle de décision est qu'il doit y avoir au moins 95% de probabilité que la valeur du mesurande soit inférieure à LSS, alors g est choisi, de sorte que pour une valeur observée de LSS+g, la probabilité que la valeur du mesurande se trouve en dessous de la limite est de 95%.
En général, la valeur de g sera une fonction de ou un simple multiple de u où u est l'incertitude standard ou combinée.
Selon la norme NF EN ISO 14253-1, le facteur multiplicateur est de 1,65 u pour obtenir une probabilité de conformité à 95%.
Dans certains cas, la règle de décision peut indiquer la valeur du multiple à utiliser.
Dans d'autres cas, la bande de garde dépendra de la valeur de P requise et de la connaissance de la distribution des valeurs probables du mesurande.
Bref, vous l'aurez compris, cette règle de décision ne peut pas être unilatérale et sous la seule responsabilité de l'OEC, une discussion et un terrain d'entente devra être trouvé pour que la règle convienne à tout le monde (OEC et client).
La typologie du laboratoire aura également une influence sur la prise de décision, un laboratoire indépendant pourra proposer systématiquement une régle de décision en défaveur du client (zone d'acceptation réduite pour limiter les risques de donner une conformité à un produit qui ne l'est pas: prise de risque acceptée par le client de se voir refuser des pièces ou un lot).
A l'inverse, un laboratoire intégré qui contrôle les produits que son usine fabrique pourra proposer une règle de décision en faveur de l'usine (zone d'acceptation élargie pour limiter les risques de refuser les produits que son usine fabrique: prise de risque acceptée par le client d'accepter des pièces potentiellement non-conformes).
Selon la norme NF EN ISO 14253-1, la prise de risque est toujours pour le fournisseur du résultat et par conséquent le laboratoire, la tolérance admissible devrait donc toujours être réduite de 1,65 u (risque plus important de déclarer un résultat non conforme).
Et l'incertitude dans tout çà, si on prend une bande de garde
= à l'incertitude, sa valeur en tant que grandeur en regard du paramètre
mesuré à toute son importance, imaginons deux laboratoires L
De plus, si l'incertitude du laboratoire est supérieure ou égale à ½ fois la tolérance spécifiée par le client, la bande de garde ne peut être qu'en dévaveur du client (zone d'acceptation élargie) car la zone d'acceptation réduite se retrouverait réduite à zéro (aucune pièce ne pouvant être déclarée bonne).
On se plaignait régulièrement que le client ne s'intéressait pas à l'incertitude de mesure, et bien, cela va changer (la communication risque d'être plus ou moins facile avec le client qui n'est pas forcément aguerri à ces notions et qui peut être perturbé pour donner son consentement sur une prise de décision qui entrainera un risque pour sa production, il peut également se sentir floué à la réception des premiers résultats surtout s'ils ne sont pas bons).
Concernant l'estimation de l'incertitude, risque également de voir des laboratoires sous-estimer certaines composantes pour réduire de manière drastique, l'incertitude élargie associée à leur résultat sous peine de perdre le client car le risque est trop important!!, ce qui serait une pratique dangereuse autant pour le client que pour l'OEC.
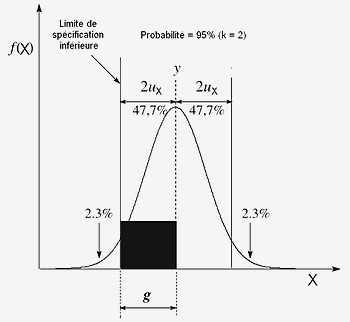
Probabilité de P=95% (k=2) d'obtenir des pièces bonnes avec une zone d'acceptation réduite.
![]()
Pour plus de précision sur la détermination des intervalles de confiance, voir fiche technique: Les intervalles de confiance.
On suppose la détermination du pH par titrimétie (soude) dans une lessive, la spécification du client est de 10,0 ± 0,5 unité pH.
| 10,2 |
9,7 |
10,3 |
10,1 |
9,8 |
10,5 |
10,0 |
9,6 |
10,4 |
9,5 |
La moyenne des 10 résultats est de 10,01 mg/l et l'écart type σ des résultats est de 0,348 mg/l
L'intervalle de confiance est donné par la relation:
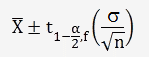
En supposant un risque α=0,05 et un degré de liberté V=n-1=10-1=9, on obtient t=2,262.
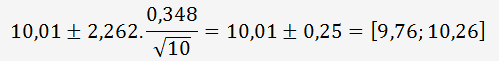
Avec EXCEL: =INTERVALLE.CONFIANCE.STUDENT(0,05;0,348;10)=0,25 (ne fonctionne qu'à partir d'EXCEL 2010)
La spécification du client étant bornée par [9,5;10,5], l'analyse de l'échantillon est conforme à la spécification.
On peut déterminer également le taux probable d'obtenir des analyses non-conformes, voir fiche technique: Les contrôles statistiques.
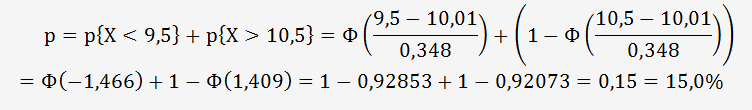
Malgré que les résultats soient conformes à la tolérance du client, il subsiste un taux probable d'obtenir 15% de valeurs non-conformes ou 85% de valeurs conformes.
C'est une information supplémentaire pour le client qu'il faudrait rajouter dans le rapport.
La décision de conformité est mentionnée dans le rapport complétée de la probabilité d’occurrence de décision correcte, par exemple : « Conforme (la fiabilité de la décision est évaluée à 85 %) ».
![]()
Tous les essais en laboratoire ne peuvent pas faire l'objet de plusieurs mesurages notamment lorsque les essais sont destructifs.
Dans ce cas, la taille de la bande de garde sera ku et la valeur de k (ou
t si l'on peut démontrer que la loi n'est pas normale) sera spécifiée
dans la règle de décision ou sera dérivée de la
distribution de probabilité des valeurs attribuées au mesurande,
qui est habituellement supposée être normale.
Dans de nombreux cas, la pratique actuelle consiste à utiliser k =
2.
En supposant que la distribution est approximativement normale, cela donne un niveau de confiance d'environ 95% qui, pour une valeur observée x, se situe dans l'intervalle x ± 2u.
Sur cette base, la probabilité que la valeur du mesurande soit inférieure
à x + 2u est d'environ 95%.
Dans le cas courant où l'on exige une preuve de conformité à
une limite supérieure, en prenant k = 2 et en exigeant une preuve de
non-conformité sans ambigüité équivaut à
régler une bande de garde g = + 2u.
On suppose un essai de traction ayant donné une résistance mécanique de 753 MPa et une spécification client sur le matériau de 745±15 MPa (730-760 MPa).
N'ayant pas plusieurs essais pour déterminer un écart-type,
nous allons prendre l'incertitude de mesure élargie associée
au résultat qui est de U
Cette incertitude élargie est déterminée pour une probabilité de 95% (K=2).
L'intervalle de confiance est donnée par la relation:
![]()
En regard de la spécification client, la valeur obtenue est conforme à la spécification.
Comme nous n'avons qu'un seul résultat, on ne peut pas savoir si la mesure suit une loi normale et si notre résultat présente un biais, nous allons donc le diminuer en retirant l'écart mesuré entre notre cellule et la cellule étalon utilisée lors de la prestation d'étalonnage pour la force concernée, le certificat montre que la cellule est en classe 0,5 et présente un biais négatif de 0,2%, il faut donc le rajouter à notre incertitude soit + 1,5 MPa.
L'ajout du biais à l'incertitude reste correcte tant que le ratio Biais/incertitude type ou combinée reste < 2. voir Biais et incertitude de mesure
Attention, ceci est un biais à l'instant t, il serait systématique si chaque année, votre cellule de force présentait toujours le même décalage et dans ce cas, l'incertitude devrait déjà en tenir compte.
Nous allons déterminer la variable centrée réduite z avec connaissance de l'incertitude avec la relation suivante:
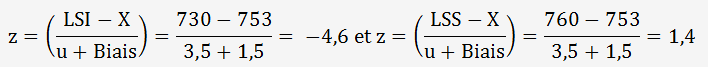
Attention, c'est l'incertitude type combinée qui est utilisée et pas l'incertitude élargie.
On en déduit les probabilités respectives:
![]()
La table des z nous donne 0,9192 pour z=1,4 et 1 pour z=4,6 donc par conséquent, la probabilité que la résistance mécanique soit conforme est égale à 91,9% et 8,1% pour qu'elle soit non-conforme.
La décision de conformité est mentionnée dans le rapport complétée de la probabilité d’occurrence de décision correcte, par exemple : « Conforme (la fiabilité de la décision est évaluée à 91,9 %) ».
Sans biais, la fiabilité de décision est de 97,7%.
Avec un biais positif, la fiabilité de décision est de 99,9%.
Si la spécification ne possede qu'une seule borne mini, l'estimation de la probabilité reste la même avec une seule borne.
On voit toute l'importance de corriger le biais à l'instant présent et d'utiliser une incertitude de mesure représentative de la méthode d'essai et de l'échantillon, la majoration systématique de toutes les composantes peut rapidement fournir une fiabilité de décision en deça de 70%.
Une feuille de calcul contenant la spécification et les résultats peut déterminer automatiquement la fiabilité de décision et la conformité de manière automatique.