Calcul du risque client et fournisseur avec EXCEL

Calcul des risques: client et laboratoire avec Excel

Lorsque l'on souhaite déterminer de manière dynamique (pour chaque essai), le risque client et fournisseur, vous devez oublier la rédaction des rapports sous WORD, cet outil bureautique n'est pas adapté à ce type de calcul et le faire séparément du rapport peut être fastidieux et en ce qui concerne les développements "maison", il faudra réserver des heures de développement informatique pour la mise au point des calculs, c'est parfaitement réalisable sous WINDEV mais tous les softs ne permettent de s'adapter aux calculs numériques.

Attention, certaines formules ne fonctionnent qu'à partir d'EXCEL 2010, il faudra donc également investir dans une mise à jour si vous souhaitez utiliser EXCEL ou utiliser des coefficients multiplicateurs fixes (si vous avez toujours le même nombre de données).

Reprenons notre exemple sur les mesures de pH:

10,2

9,7

10,3

10,1

9,8

10,5

10,0

9,6

10,4

9,5

La moyenne est y0=10,01: =MOYENNE(Plage des données), l'écart-type vaut σ=0,348: =ECARTYPE(Plage des données).

l'incertitude de type A vaut um=±0,11, on peut la déterminer automatiquement avec la fonction: =INTERVALLE.CONFIANCE.NORMALE(0,05;0,348;10), le risque est α=0,05 (95% de probabilité); l'écart-type est de 0,348 et le nombre de valeur est n=10.

INTERVALLE.CONFIANCE.NORMALE(0,05;0,348;10)=0,22 (il s'agit de l'écart-type multiplié par un facteur d'élargissement k=1,96)

Mais on pourrait considérer que rien ne peut m'affirmer que nous sommes en présence d'une loi normale et préférer prendre une loi de STUDENT:

INTERVALLE.CONFIANCE.STUDENT(0,05;0,348;10)=0,25 (il s'agit de l'écart-type dégradé et multiplié par un facteur d'élargissement t=2,262) ATTENTION (Formule ne fonctionnant qu'à partir d'EXCEL 2010, elle n'existe pas dans les versions antérieures).

Les bornes sont réduites d'une bande de garde équivalent à la moitié de l'incertitude soit [TRL=9,56;TRS=10,44].

La zone de tolérance du client est [TL=9,5;TS=10,5].

L'étendue de la plage réduite w=10,44-9,56=0,88 = 4Um.

Le risque client est donné par la relation suivante:

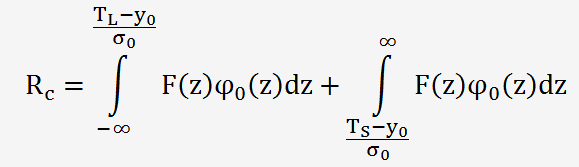
Avec les bornes Z1 et Z2:

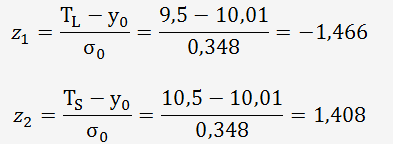
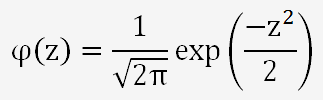
La fonction φ0(z) (loi normale centrée réduite) est exprimé en fonction de z et se traduit par:

F(z) est une fonction de probabilité qui s'exprime par:

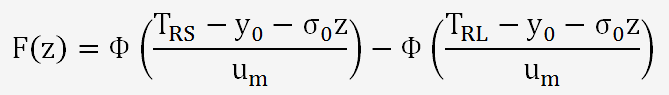
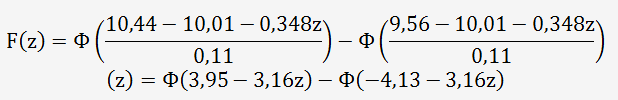
Au format EXCEL, cela devient:

F(z)φ(z)=(LOI.NORMALE.STANDARD(3,95-3,16z)-LOI.NORMALE.STANDARD(-4,13-3,16z))*(1/(RACINE(2*PI())))*EXP(-0,5*z^2)

Z représentant les bornes entre -∞ et -1,466 et 1,408 et +∞.

Excel ne faisant pas de calcul d'intégrale, nous allons utiliser la méthode de SIMPSON, cela consiste à fragmenter l'intégrale avec un incrément qui dépend des bornes et du nombre de réitération que l'on souhaite (des simulations démontrent qu'une vingtaine de réitération suffisent à déterminer un résultat cohérent).

Pour la première intégrale, nous allons intégrer entre [a=-5;b=-1,466] avec 20 réitérations.

L'incrément se détermine de la manière suivante:

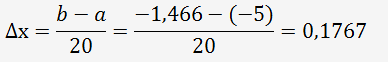
Nous allons déterminer les résultats de la fonction entre [a=-5;b=-1,466] pour chaque incrément:

avec a1=-5, a2=a1+Δx, a3=a2+Δx,..................a20=a19+Δx

b1=a1+Δx, b2=a2+Δx, b3=a3+Δx,...............b20=a20+Δx

c1=(a1+b1)/2, C2=(a2+b2)/2, C3=(A3+B3)/2,....................c20=(a20+b20)/2

Le résultat de l'intégrale s'obtient avec la formule suivante:

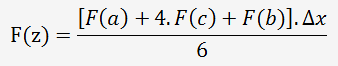
Tableau des résultats (volontairement arrondis)

n	a	b	c	F(a)	F(b)	F(c)	[F(a)+4F(c)+F(b)].Δx/6
1	-5	-4,823	-4,911	0	0	0	0
2	-4,823	-4,646	-4,735	0	0	0	0
3	-4,646	-4,469	-4,558	0	0	0	0
4	-4,469	-4,293	-4,381	0	0	0	0
5	-4,293	-4,116	-4,204	0	0	0	0
6	-4,116	-3,939	-4,028	0	0	0	0
7	-3,939	-3,763	-3,851	0	1,37E-18	1,06E-19	5,31E-20
8	-3,763	-3,586	-3,675	0	1,86E-16	1,67E-17	7,50E-18
9	-3,586	-3,409	-3,498	0	1,79E-14	1,90E-15	7,57E-16
10	-3,409	-3,233	-3,321	0	1,23E-12	1,54E-13	5,49E-14
11	-3,233	-3,056	-3,144	0	6,02E-11	8,97E-12	2,87E-12
12	-3,056	-2,879	-2,968	0	2,11E-09	3,72E-10	1,08E-10
13	-2,879	-2,703	-2,791	0	5,31E-08	1,10E-08	2,92E-09
14	-2,703	-2,526	-2,614	0,0000001	9,59E-07	2,35E-07	5,75E-08
15	-2,526	-2,349	-2,438	0,0000010	1,25E-05	3,60E-06	8,20E-07
16	-2,349	-2,173	-2,261	0,0000125	0,000117394	3,98E-05	8,51E-06
17	-2,173	-1,996	-2,084	0,0001174	0,000803384	0,000319436	6,47E-05
18	-1,996	-1,819	-1,908	0,0008034	0,004030261	0,001869487	0,000362561
19	-1,819	-1,642	-1,731	0,0040303	0,014989417	0,008061568	0,001509719
20	-1,642	-1,466	-1,554	0,0149894	0,0149894	0,025965736	0,004737452
TOTAL (Somme de la dernière colonne)=INT(1)							0,0066839

Pour la seconde intégrale, nous allons intégrer entre [a=1,408;b=5] avec 20 réitérations.

L'incrément se détermine de la manière suivante:

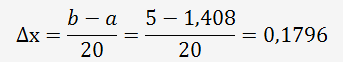
Nous allons déterminer les résultats de la fonction entre [a=1,408;b=5] pour chaque incrément:

Tableau des résultats (volontairement arrondis)

n	a	b	c	F(a)	F(b)	F(c)	[F(a)+4F(c)+F(b)].Δx/6
1	1,408	1,588	1,498	0,04566871	0,01613932	0,028112051	0,005214227
2	1,588	1,767	1,678	0,01613932	0,00426068	0,008611619	0,00164144
3	1,767	1,947	1,857	0,00426068	0,00082539	0,0001950892	0,00038576
4	1,947	2,127	2,037	0,00082539	0,000115971	0,000322248	6,67E-05
5	2,127	2,306	2,217	0,000115971	1,17E-05	3,84E-05	8,42E-06
6	2,306	2,486	2,396	1,17E-05	8,47E-07	3,28E-06	7,70E-07
7	2,486	2,665	2,575	8,47E-07	4,36E-08	2,00E-07	5,07E-08
8	2,665	2,845	2,755	4,36E-08	1,60E-09	8,72E-09	2,40E-09
9	2,845	3,025	2,935	1,60E-09	4,14E-11	2,68E-10	8,12E-11
10	3,025	3,204	3,114	4,14E-11	7,61E-13	5,86E-12	1,96E-12
11	3,204	3,384	3,294	7,61E-13	9,87E-15	9,05E-14	3,39E-14
12	3,384	3,563	3,474	9,87E-15	9,03E-17	9,86E-16	4,16E-16
13	3,563	3,743	3,653	9,03E-17	5,83E-19	7,58E-18	3,63E-18
14	3,743	3,922	3,833	5,83E-19	0	0	0
15	3,922	4,102	4,012	0	0	0	0
16	4,102	4,282	4,192	0	0	0	0
17	4,282	4,461	4,371	0	0	0	0
18	4,461	4,640	4,551	0	0	0	0
19	4,640	4,820	4,731	0	0	0	0
20	4,820	5	4,910	0	0	0	0
TOTAL (Somme de la dernière colonne)=INT(2)							0,0073174

Calcul du risque client:

Le risque de l'OEC (Laboratoire) s'exprime par la relation suivante:

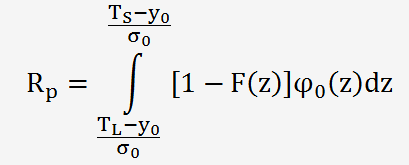
Au format EXCEL, cela devient:

(1-F(z))φ(z)=(1-(LOI.NORMALE.STANDARD(3,95-3,16z)-LOI.NORMALE.STANDARD(-4,13-3,16z)))*(1/(RACINE(2*PI())))*EXP(-0,5*z^2)

Nous allons déterminer les résultats de la fonction entre [a=-1,466;b=1,408] pour chaque incrément:

L'incrément se détermine de la manière suivante:

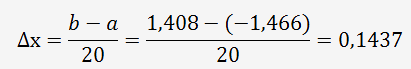
Tableau des résultats (volontairement arrondis)

n	a	b	c	F(a)	F(b)	F(c)	[F(a)+4F(c)+F(b)].Δx/6
1	-1,4661	-1,3224	-1,3943	0,0941677	0,0862200	0,0916849	0,0131073
2	-1,3224	-1,1786	-1,2505	0,0862200	0,0679661	0,0780963	0,0111775
3	-1,1786	-1,0349	-1,1068	0,0679661	0,0452786	0,0567091	0,0081472
4	-1,0349	-0,8911	-0,9630	0,0452786	0,0251355	0,0345388	0,0049966
5	-0,8911	-0,7474	-0,8193	0,0251355	0,0115064	0,0174307	0,0025481
6	-0,7474	-0,6037	-0,6755	0,0115064	0,0043105	0,0072242	0,0010712
7	-0,6037	-0,4599	-0,5318	0,0043105	0,0013140	0,0024427	0,0003688
8	-0,4599	-0,3162	-0,3881	0,0013140	0,0003247	0,0006706	0,0001035
9	-0,3162	-0,1724	-0,2443	0,0003247	0,0000661	0,0001494	0,0000237
10	-0,1724	-0,0287	-0,1006	0,0000661	0,0000208	0,0000305	0,0000050
11	-0,0287	0,1149	0,0431	0,0000208	0,0000666	0,0000306	0,00000050
12	0,1149	0,2587	0,1868	0,0000666	0,0003301	0,0001512	0,00000240
13	0,2587	0,4024	0,3306	0,0003301	0,0013470	0,0006846	0,0001058
14	0,4024	0,5462	0,4743	0,0013470	0,0044553	0,0025144	0,0003800
15	0,5462	0,6899	0,6180	0,0044553	0,0119919	0,0074979	0,0011125
16	0,6899	0,8337	0,7618	0,0119919	0,0264133	0,0182412	0,0026681
17	0,8337	0,9774	0,9055	0,0264133	0,0479753	0,0364449	0,0052745
18	0,9774	1,1212	1,0493	0,0479753	0,0726116	0,0603354	0,0086706
19	1,1212	1,2651	1,1930	0,0726116	0,0928776	0,0837797	0,0119929
20	1,2651	1,4086	1,3368	0,0928776	0,1022808	0,0991734	0,0141788
TOTAL (Somme de la dernière colonne)=INT(3)							0,0860

Calcul du risque Laboratoire:

Résultats avec une bande de garde = 50% de l'incertitude type

Résultats avec une bande de garde = 100% de l'incertitude type

Résultats avec une bande de garde = 100% de l'incertitude Elargie (Norme ISO 14253-1)

Résultats avec une bande de garde = 100% de l'incertitude Elargie (Loi supposée non normale et Norme ISO 14253-1)

On pourrait également intégrer en prenant une fonction de type Loi de Student qui utilise la fonction Gamma (les calculs deviennent plus compliqués et il faut une version EXCEL 2016, car la loi GAMMA ne fonctionne pas sur des données négatives dans les versions antérieures, d'ou de nombreuses conditions en fonction du signe du résultat de la fonction).