Carte de contrôle avec surveillance par outils statistiques
Tous les laboratoires utilisent des cartes de contrôle pour surveiller une dérive éventuelle d'un processus de mesurage mais si on veut respecter les quelques règles applicables à ces cartes (voir Cartes de contrôle), on se rend vite compte que rapidement l'une de ces règles n'est pas respectée, notre processus est-il pour autant mauvais?, doit-on rechercher la cause racine de ce problème?, faut-il refaire des mesurages pour enrayer la situation?, bref, une perte de temps significative alors que les résultats sont toujours entre les bornes que s'est fixé le laboratoire.
Méthodologie :
On supposera que le laboratoire souhaite vérifier périodiquement la dérive d'un équipement à partir d'une solution ou d'un matériau de référence, les bornes maxi et mini étant fournies dans un document normatif sous la forme d'un EMT relatif mais cela pourrait être à partir de bornes calculées ou fixées par le laboratoire.
Je vous propose de réaliser une carte de contrôle dynamique qui repose sur 4 règles de décision et qui utilisera le tableur EXCEL:
Les règles de décision pour déclarer que la vérification périodique des mesurages satisfasse à nos exigences sont :
- L’ensemble des valeurs obtenues doit être compris dans l’intervalle
de tolérance imposé par le document normatif (ASTM, ISO ou autre)
ou les exigences internes.
- La pente de la courbe de tendance (coefficient directeur) doit être
inférieure à la pente maximale qui pourrait éventuellement
conduire à des valeurs en dehors de la tolérance.
- La probabilité d’obtenir des résultats dans la tolérance
doit être supérieure à 90 % (critère que l'on pourra
ajuster en fonction des résultats).
- La carte doit contenir au moins 30 valeurs pour pouvoir exploiter l’analyse
des tendances et les tests de normalité (droite de Henry et Shapiro-wilk)
devront démontrer que la distribution des données suit une loi
normale.
Cette distribution normale n’est possible que si la résolution
de lecture permet de donner un large éventail de valeurs au regard
de la tolérance imposée.
Les 30 points correspondent à la mise en œuvre de la carte de
contrôle (10 points pour chaque opérateur (x2) par exemple: soit
20 points) + 5 vérifications périodiques (2 x 5 points).
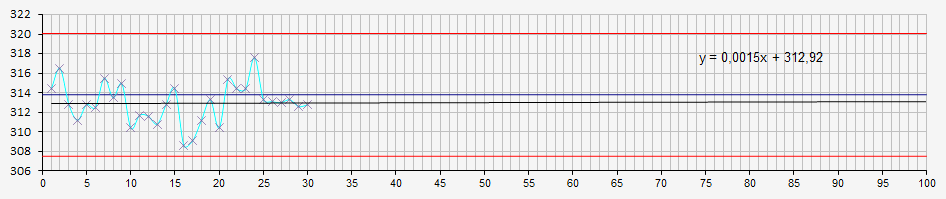
On supposera que la carte puisse contenir 100 valeurs dans l'exemple.
Données numériques:
La solution de référence ou le matériau de référence à une valeur nominale fournie dans son certificat de 313,8 (pas d'unité précisée pour l'exemple) associée à une incertitude élargie de 1,57.
La norme impose une erreur relative de ± 2% de la valeur de référence soit un EMT: Ecart maximal Toléré de [307,4;320,08].
Pente de la courbe de tendance:
Considérons les points suivants (volontairement choisis avec un nombre < 30): 16 valeurs.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 314,4 | 316,5 | 312,8 | 311,2 | 312,8 | 312,5 | 315,5 | 313,5 |
314,9 | 310,4 | 311,7 |
311,6 | 310,8 | 312,8 |
314,4 |
308,6 |
La pente maximale s’obtient à partir des données en abscisse
[0:100] : nombre de points sur une carte et des données en abscisse
[valeur étalon:valeur tolérance supérieure] soit [313,8:320,08].
La pente en valeur absolue des données Pd est obtenue par :=ABS(PENTE(Plage
des ordonnées ; Plage des Abscisses))=ABS(PENTE(16 valeurs;0:100))=0,2121.
La pente maximale Pm est obtenue par :=PENTE(valeur étalon:valeur tolérance
supérieure;0:100)=PENTE([313,8:320,08;0:100)=0,06276.
Les données sont satisfaisantes si : Pd ≤ Pm.
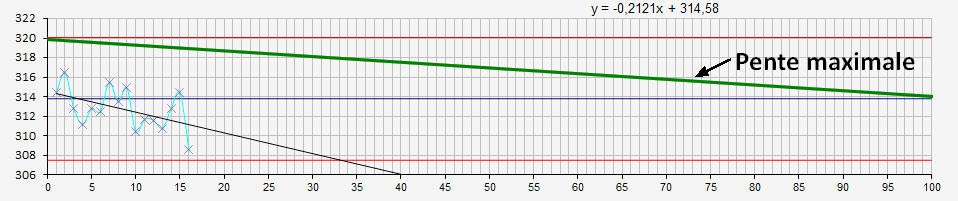
Dans le cas présent, l'inégalité n'est pas respectée et la carte n'est pas conforme.
Probabilité des résultats d’être dans la tolérance :
L'écart-type sur les 16 valeurs est de 2,06.
Elle est déterminée par : =LOI.NORMALE(Tolérance supérieure;Valeur
certifiée;Ecart-type de la série;VRAI = fonction cumulative)-LOI.NORMALE
Tolérance inférieure;Valeur certifiée;Ecart-type de la
série;VRAI = fonction cumulative)=LOI.NORMALE(320,08;313,8;2,06;VRAI)-LOI.NORMALE(307,4;Valeur
certifiée313,8;2,06;VRAI)=0,998=99,8%.
Les données sont satisfaisante si : P(Φ) > 90%, ce qui est
le cas.
Test de normalité :
Droite de Henry et Test de shapiro-Wilk
La droite de Henry est une présentation graphique permettant d’évaluer la « normalité » d’une distribution.
Principe: la courbe des fréquences cumulées est une
droite si la distribution statistique suit une Loi Normale (courbe en forme
de cloche ou courbe de Gauss).
La droite de Henry correspond aux fréquences théoriques cumulées
tirées de la table de la Loi Normale.
Les points indiquent les valeurs des fréquences réelles cumulées
pour les différentes valeurs de la variable.
Si la distribution des valeurs réelles de la variable était
parfaitement “normale”, tous les points se trouveraient sur la
droite de Henry.
Nous allons reprendre nos 16 points + d'autres pour obtenir les 30 valeurs:
| Nb |
Valeurs |
Ordre croissant | Proportion
cumulative |
Z score | Moyenne |
| 1 | 314,4 | 308,6 | 1/31 | -1,849 | 312,94 |
| 2 | 316,5 | 309,1 | 2/31 | -1,518 | Ecart-Type |
| 3 | 312,8 | 310,4 | 3/31 | -1,300 | 2,04 |
| 4 | 311,2 | 310,4 | 4/31 | -1,131 | Coefficient de correlation |
| 5 | 312,8 | 310,8 | 5/31 | -0,989 | 0,989 |
| 6 | 312,5 | 311,2 | 6/31 | -0,865 | Valeur critique avec α=0,05 |
| 7 | 315,5 | 311,2 | 7/31 | -0,753 | 0,927 |
| 8 | 313,5 | 311,6 | 8/31 | -0,649 | |
| 9 | 314,9 | 311,7 | 9/31 | -0,552 | |
| 10 | 310,4 | 312,5 | 10/31 | -0,460 | |
| 11 | 311,7 | 312,6 | 11/31 | -0,372 | |
| 12 | 311,6 | 312,8 | 12/31 | -0,287 | |
| 13 | 310,8 | 312,8 | 13/31 | -0,204 | |
| 14 | 312,8 | 312,8 | 14/31 | -0,122 | |
| 15 | 314,4 | 312,8 | 15/31 | -0,040 | |
| 16 | 308,6 | 313,0 | 16/31 | 0,040 | |
| 17 | 309,1 | 313,1 | 17/31 | 0,122 | |
| 18 | 311,2 | 313,3 | 18/31 | 0,204 | |
| 19 | 313,3 | 313,3 | 19/31 | 0,287 | |
| 20 | 313,3 | 313,3 | 20/31 | 0,372 | |
| 21 | 315,4 | 313,5 | 21/31 | 0,460 | |
| 22 | 314,4 | 314,4 | 22/31 | 0,552 | |
| 23 | 314,4 | 314,4 | 23/31 | 0,649 | |
| 24 | 317,6 | 314,4 | 24/31 | 0,753 | |
| 25 | 313,3 | 314,4 | 25/31 | 0,865 | |
| 26 | 313,1 | 314,9 | 26/31 | 0,989 | |
| 27 | 313,0 | 315,4 | 27/31 | 1,131 | |
| 28 | 313,3 | 315,5 | 28/31 | 1,300 | |
| 29 | 312,6 | 316,5 | 29/31 | 1,518 | |
| 30 | 312,8 | 317,6 | 30/31 | 1,849 |
Données en ordre croissant de manière automatique:
Les données sont triées pour les mettre dans
un ordre croissant avec la relation suivante :
=SIERREUR(PETITE.VALEUR(plage de valeur;N° de ligne);#N/A)=SIERREUR(PETITE.VALEUR(314,4
à 312,8;1);#N/A) pour 308,6 puis =SIERREUR(PETITE.VALEUR(314,4 à
312,8;2);#N/A) pour 309,1 .......................=SIERREUR(PETITE.VALEUR(314,4
à 312,8;30);#N/A) pour 317,6.
Le tableur recherche la plus petite valeur sur la colonne des valeurs (100
valeurs maxi dans l'exemple) et les replace par rapport au rang d’origine
(308,6 = Rang 1) et si la cellule ne contient pas de valeurs, elle affiche
#N/A.
Proportion cumulative :
Première cellule=SI(ET(TYPE(valeur croissante)=1;valeur croissante<>"");1/(Nb de valeurs+1);"")=SI(ET(TYPE(308,6)=1;308,6<>"");1/(30+1);"")=1/31.
Seconde cellule et jusqu'à la dernière cellule= SI(ET(TYPE(seconde valeur croissante)=1;seconde valeur croissante<>"");1/(Nb de valeurs+1)+premièce cellule de proportion cumulative;"")=SI(ET(TYPE(309,1)=1;309,1<>"") ;1/(30+1)+(1/31);"")=2/31.................=SI(ET(TYPE(317,6)=1;317,6<>"");1/(30+1)+(29/31);"")=30/31.
Nb de valeur = =NB(plage de valeurs)
En pratique, on augmente l’effectif total d’une unité
(+1) pour que la Loi normale inverse puisse être calculée sur
la valeur x maximale.
Elle s’applique pour chaque valeur.
1ere ligne : si la valeur est numérique, renvoi la valeur 1 et si le contenu est différent d’une cellule vide, alors on calcule 1/ (Nombre de valeurs=30 +1), si le contenu de la cellule n’est pas numérique et qu’elle n’est pas vide, afficher une cellule vide.
Loi normale inverse : Z Score
Renvoie, pour une probabilité donnée (Proportion cumulative), la valeur d’une variable aléatoire suivant une loi normale standard (ou centrée réduite).
Cette distribution a une moyenne égale à zéro et un
écart type égal à 1.
Loi normale inverse = SI(ET(TYPE(proportion cumulative)=1;proportion cumulative<>"");LOI.NORMALE.STANDARD.INVERSE(proportion
cumulative);"") = SI(ET(TYPE(1/31)=1;1/31<>"");LOI.NORMALE.STANDARD.INVERSE(1/31);"")=-1,849..............=SI(ET(TYPE(30/31)=1;30/31<>"");LOI.NORMALE.STANDARD.INVERSE(30/31);"")
=1,849.
Elle s’applique pour chaque valeur.
1ere ligne : si la valeur de proportion cumulative en 1/31 est numérique, renvoi la valeur 1 et si le contenu est différent d’une cellule vide, alors on calcule LOI.NORMALE.STANDARD.INVERSE(1/31) = -1,849 ; si le contenu de la cellule n’est pas numérique et qu’elle n’est pas vide, afficher une cellule vide.
Graphique représentant la droite de Henry (ordonnée = loi normale inverse et abscisse = valeurs mesurées).
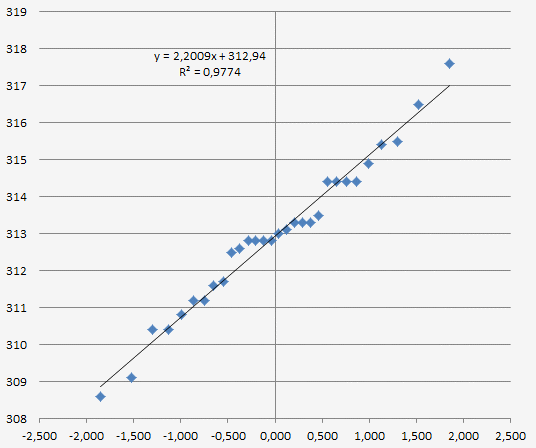
Les points sont alignés sur une droite, la distribution
suit une loi normale.
La droite coupe l’axe des ordonnées à la valeur moyenne
des résultats = b = 312,9 sur la droite.
La droite coupe l’axe des abscisses à la valeur de l’écart-type
= a = 2,2 sur la droite.
Test de Shapiro-Wilk
Ce test est fondé sur le rapport W de deux estimations liées
à la variance de la population dont provient l´échantillon
: l´une, fonction des étendues partielles xn - x1, xn-1 - x2,
..., que l´on peut déduire de la suite ordonnée (x1 ≤
x2 ≤ ... ≤ xj ≤ ... ≤ xn) des n observations indépendantes
dun échantillon d'effectif n, l'autre, z², fonction des carrés
des écarts à la moyenne x des observations.
Z s’obtient en déterminant le coefficient de corrélation
entre les valeurs de dureté en ordre croissant et les valeurs des Z
scores.
=COEFFICIENT.CORRELATION(Plage de valeurs croissantes;plage des Z score)= COEFFICIENT.CORRELATION(308,6:317,6;-1,849:1,849)=0,989
D'autres colonnes ont été créées avec une condition pour éviter de calculer les colonnes avec des #N/A que le tableur ne comprend pas.
=SIERREUR(valeur croissante;"")=SIERREUR(308,6;"")=308,6
=SIERREUR(SI(ET(TYPE(Zscore)=1;Zscore<>"");LOI.NORMALE.STANDARD.INVERSE(Zscore));"")=SIERREUR(SI(ET(TYPE(-1,849)=1;-1,849<>""); LOI.NORMALE.STANDARD.INVERSE(-1,849));"")=-1,849
La distribution de W, lorsque l´hypothèse de normalité
est vérifiée, a été tabulée et la table
de Shapiro-Wilk donne, en fonction de n, les valeurs Wα
telles que ;
Pr (W < Wα) = α
pour α = 0,05.
La table donne les valeurs Wα conduisant
au rejet de l´hypothèse de normalité, au risque α
= 0,05 de rejeter une hypothèse vraie.
L'hypothèse de normalité est rejetée si W est inférieur
à la valeur Wα correspondant à
n et a.
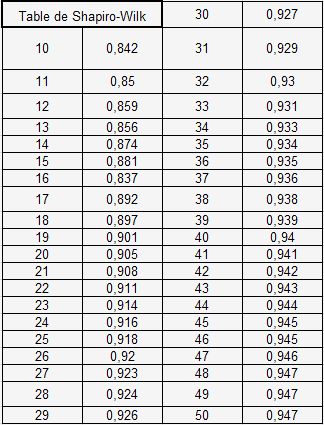
Wα s’obtient avec la table de Shapiro-Wilk, avec la fonction rechercheV :
=SI(Nb de valeur<=50;RECHERCHEV(Nb de valeur;Plage des valeur de Wα;2;);0,947)=SI(30<=50;RECHERCHEV(30;Plage des valeur de Wα;2;);0,947)=0,927
Attention: les valeurs de wα doivent
être sur une même colonne pour que la fonction RECHERCHEV fonctionne.
Si le nombre de valeur est < 50 ; on recherche dans la table pour la valeur
n = 30, le coefficient correspondant : 0,927, si le nombre de valeur est >
50, le coefficient est toujours égal à 0,947.
Wα=0,927 et W=0,989 avec Wα<
W, les valeurs suivent une loi normale.
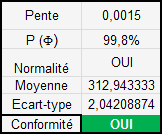
Règles de décision :
Pd est obtenue par : =ABS(PENTE(Plage des ordonnées; Plage des Abscisse))
=ABS(PENTE(30 valeurs;0:100))=0,0015.
Pm est obtenue par : =PENTE([313,8 ; 313,8 + 2%=320,1]; [0 ;100] )=0,06276
Les données sont satisfaisantes si : Pd ≤ Pm (la marge correspond
à peu près à trois points consécutif à
318).
Probabilité=LOI.NORMALE(320,08;313,8;2,04;VRAI)-LOI.NORMALE(307,5;313,8;2,04
;VRAI) = 0,998 soit 99,8 %.
Les données sont satisfaisante si : P(Φ) > 90%.
Les données suivent une loi normale, la probabilité et la pente
sont conformes au critère, aucun point à l’extérieur
des tolérances normatives, l’analyse de la tendance de la carte
de contrôle est satisfaisante.