En apprendre un peu plus sur les essais de traction
Notions générales:
- Propriétés multiples après essai
- Caractérise la résistance mécanique et la ductilité
d'un matériau
- Relation avec la dureté dans une certaine mesure et avec précaution
- Essais destructifs
- Le caractère conventionnel des mesures oblige pour conserver la reproductibilité
et la fidélité de suivre des modes opératoires très
précis.
Principe:
L'essai de traction consiste à exercer, sur une éprouvette, des forces croissantes qui vont la déformer progressivement puis la rompre.
En pratique, les essais sont pilotés par la vitesse de déformation (traverse ou extensomètre).
On reporte la force mesurée en fonction de l'allongement de l'éprouvette, ce qui donne une courbe de traction.
La courbe de traction:
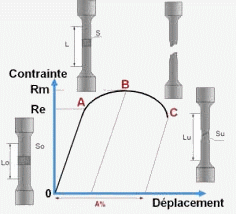
Sur une courbe de traction (force-déformation), on observe les phases successives suivantes:
- Entre les points 0 et A, une phase élastique où la déformation est réversible,
- de A à B, une déformation permanente homogène appelée aussi déformation plastique répartie,
- de B à C, la déformation plastique se localise dans une petite portion de l'éprouvette et n'est plus homogène, c'est la striction, on aboutit à la rupture en C.
La résistance à la traction:
Cette grandeur est parfaitement définie puisque c'est le quotient de la charge maximale par la section initiale de l'éprouvette.
Il faut noter qu'il ne s'agit pas d'une mesure au moment de la rupture.
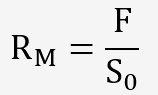
La surface sera représentative de la forme de l'éprouvette: circulaire, plate, tube,...
La limite d'élasticité:
On peut distinguer 2 types de courbes de traction suivant la présence ou pas d'un seuil d'écoulement:
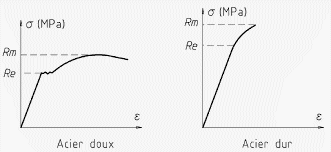
La première courbe correspond à des aciers ferritiques en général (le Titane recuit également) mais peut se présenter avec moins de netteté pour des aciers plus durs.
La seconde courbe avec une transition plus progressive correspond aux aciers durs ou aux aciers austénitiques.
Quand la limite est marquée par un palier de charge, la mesure ne semble pas trop poser de problèmes, alors que le passage progressif nécessite l'utilisation de limites conventionnelles.
Les différentes valeurs mesurables sont:
- La limite d'élasticité supérieure ReH
- La limite d'élasticité inférieure ReL
- et éventuellement, la longueur du palier en %.
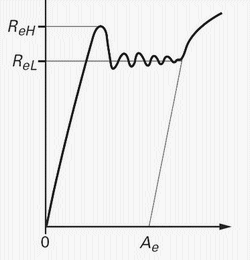
La limite supérieure dépend de la forme de l'éprouvette, de son état de surface, des conditions d'essais et de la machine d'essai, d'où une certaine dispersion qui ne permet de l'utiliser sauf comme limite apparente dans les essais de routine.
La limite inférieure est moins sensible aux défauts géométriques de l'éprouvette, mais le palier est rarement horizontal en raison de la propagation des bandes de Lüders:

Le phénomène du palier correspond à une déformation hétérogène de l'éprouvette, c'est à dire à la naissance d'une petite zone déformée locale, en général près des têtes de l'éprouvette, qui se propage ensuite à toute l'éprouvette.
Pendant le palier, la zone déformée va s'étendre progressivement à toute l'éprouvette et la charge recommencera à croitre quand toute l'éprouvette se sera déformée d'une façon homogène.
Le taux de déformation local en % est égal à la longueur du palier, c'est-à-dire que si on observe un palier de 4% de long, une éprouvette arrêtée au milieu du palier n'est pas allongée de 2% mais la moitié de l'éprouvette est déformée de 4% et l'autre non déformée plastiquement (compte tenu de la déformation élastique).
Le front ou les fronts de la zone déformée, qui progressent, ont des formes géométriques simples, ce sont généralement des droites et s'il y a plusieurs fronts, on observe tout un réseau de lignes que l'on désigne sous le nom de lignes de Piobert-Lüders ou Hartmann-Lüders.
Tant que les bandes n'ont pas envahi toute l'éprouvette, la charge reste sensiblement constante d'où le palier, les fluctuations de la charge correspondent à la naissance de nouvelles bandes.
La fin du palier correspond à la jonction des bandes, l'angle moyen est de 51° avec l'axe de traction (mécanisme de déformation par cisaillement).
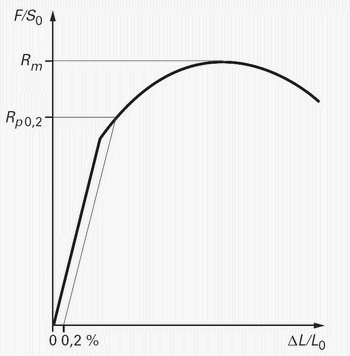
Lorsque qu'il y a passage progressif de l'élasticité linéaire à la déformation plastique, l'amplification sur la courbe du phénomène met en évidence le manque de linéarité de la montée élastique pour des raisons d'imperfection d'éprouvette et de non-respect de la loi de HOOKE.
Il est donc préférable de définir des limites conventionnelles avec lesquelles, on peut mesurer avec précision l'allongement, comme 0,2 % par exemple.
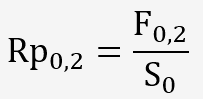
L'allongement:
L'allongement total de l'éprouvette est l'allongement à la rupture:
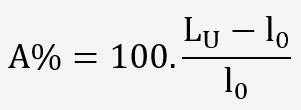
L
L
En général, les éprouvettes sont dites "proportionnelles"
et pour les éprouvettes cylindriques: L
Cet allongement est la somme de l'allongement réparti A
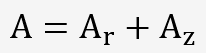
La striction:
La striction est la réduction de section maximale de l'éprouvette rompue (section de rupture):
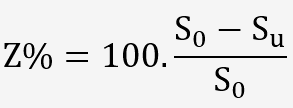
S
S
Proportionnalité:
Dans la première portion de la courbe, il y-a proportionnalité entre charge et déformation (au moins en première approximation), c'est la loi de HOOKE, la caractéristique est la pente de cette droite qui est le module d'élasticité.
L'essai de traction n'est pas assez précis en général pour la mesure du module d'élasticité.
Constantes d'élasticité:
E: désigne le module d'élasticité ou module d'Young et exprime le rapport entre la charge unitaire appliquée et la déformation longitudinale de l'éprouvette.
ν: le coefficient de Poisson exprime le rapport entre la déformation longitudinale de l'éprouvette et la déformation transversale (vaut 0,30 pour les aciers).
G: le Module de cisaillement exprime le rapport entre le couple et la déformation par cisaillement (essai de torsion: module de Coulomb ou de Lamé).
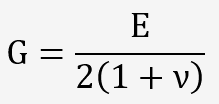
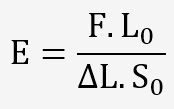
Variation du volume dans le domaine élastique:
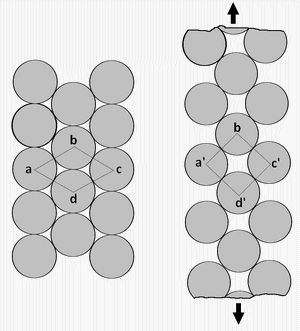
Si on considère un élément de volume
parallélépipédique: V
On peut écrire:
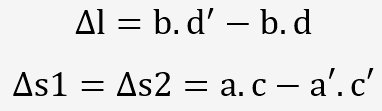
Un effort F appliqué de manière axiale entraine un effort unitaire:
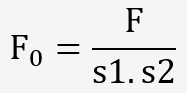
Pour chaque composante du volume, on peut écrire:
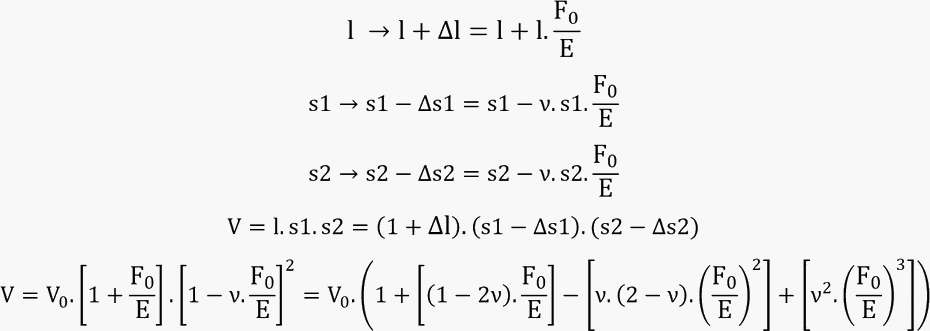
On sait que E est toujours très grand devant F
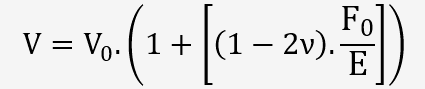
On constate que si ν vaut 0.5, le volume reste constant dans la phase élastique, cependant, pour les matériaux cristallins, ν est inférieur à 0.5 (1-2ν)>0, par conséquent, sous un effort unidirectionnel, la déformation élastique s'accompagne d'une augmentation réversible de son volume.
Les courbes rationnelles:
Comme le montre la définition, la charge de rupture est une grandeur conventionnelle puisque l'on rapporte la charge maximale à la section initiale, ce qui empêche de tenir compte de la section réelle dans les calculs.
La contrainte vraie σ correspond à la charge rapportée à la section instantanée, soit:
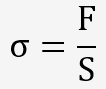
Avec F: Charge appliquée et S: section instantanée.
De même, l'allongement ordinaire n'est pas additif, ce qui est également gênant pour les calculs de plasticité, on le remplace par la déformation rationnelle:
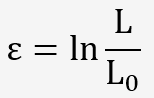
Ceci n'est évidemment valable que dans la zone des allongements répartis et à condition que l'homogénéité de la déformation de la partie calibrée sur la base de mesure soit acceptable.
Cette déformation rationnelle diffère peu de l'allongement ordinaire et pour les faibles valeurs, si on l'exprime en %, elle se définit par la relation:
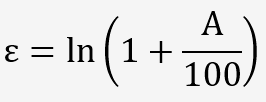
La différence ne dépasse pas 2% pour une déformation de 20%, mais l'écart augmente pour les déformations plus importantes.
L'avantage de cette définition des déformations est l'additivité, si l'on considère les déformations ε1, ε2, ε3 dans les 3 axes (x, y, et z) principaux d'une éprouvette ou d'un élément d'une pièce, on a toujours dans le domaine plastique:
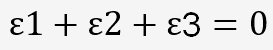
Ce qui traduit la constance du volume.
On va donc reporter sur le graphique, la contrainte vraie σ en fonction de la déformation rationnelle ε, c'est la courbe rationnelle de traction.
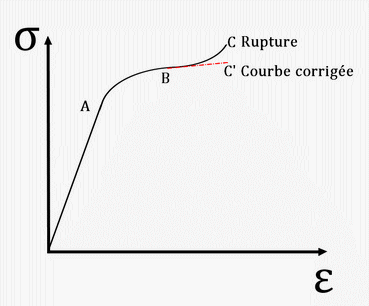
Sur cette courbe, il n'y a pas de différence avec le tracé ordinaire pour la partie élastique et la limite d'élasticité, car les déformations sont très petites.
Entre la limite d'élasticité A et le point B correspondant à la charge maximale, la courbe à une forme parabolique.
Au-delà du point B et jusqu'à la rupture en C, l'existence de la striction complique le calcul de la contrainte vraie car il faut tenir compte de l'effet de concentration de contrainte.
La formule de correction la plus utilisée est celle de BRIDGMANN:
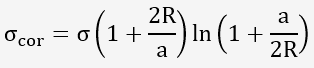
Avec a: rayon de la section minimale et R: rayon de courbure de la zone de striction
Après correction, cette partie de la courbe rationnelle peut être considérée comme sensiblement linéaire.
Le coefficient d'écrouissage:
La portion d'allure parabolique de la courbe rationnelle peut être mise sous forme mathématique.
L'expression la plus utilisée s'exprime de la manière suivante:
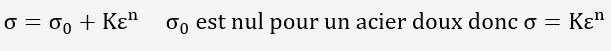 (1)
(1)
n est appelé coefficient d'écrouissage.
Une des propriétés importantes de cette équation est l'égalité entre n et la valeur d'allongement réparti, à la charge maximale, n = σ.
Sur la courbe rationnelle, le point d'instabilité est défini par la tangente dont la pente:
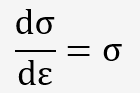
Ceci quel que soit l'équation de la courbe rationnelle.
Pour l'équation (1), cela donne:
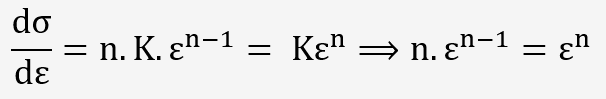
A la charge maximale, l'égalité est vérifiée si n = ε.
Pour déterminer n, une des méthodes est basée sur le tracé de la courbe rationnelle en coordonnées logarithmique, si on reporte log σ en fonction de log ε, on obtient:
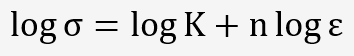
c'est à dire une droite de coefficient directeur n si la loi est vérifiée.
une des méthodes consiste à déterminer log σ pour deux valeurs d'allongement et la pente de la droite donne n (méthode de NELSON-WINLOCK).
Le coefficient d'anisotropie:
Les théories classiques de l'élasticité et de la plasticité supposent que le métal se déforme d'une façon homogène et isotrope.
Or dans le cas d'un palier, l'homogénéité des déformations n'est plus respectée.
Etant donné les diverses possibilités de déformation par glissement sur les plans cristallographiques, les monocristaux ne sont pas isotropes, ils ne donnent donc pas des courbes de traction identiques suivant la direction de l'effort.
Ce phénomène n'est pas visible pour les aciers dans lesquels, les cristaux sont des orientations aléatoires et la mesure globale ne dépend pas de la direction de l'effort.
Ce n'est plus le cas si des traitements thermomécaniques favorisent une direction privilégiée (texture ou fibrage).
Cette anisotropie se manifeste par des différences de propriétés suivant la direction de prélèvement des éprouvettes par rapport à la direction de laminage d'une tôle par exemple et si les différences sur les caractéristiques classiques (limite d'élasticité, résistance, allongement à rupture) sont relativement faibles, il n'est est pas de même pour la répartition des déformations suivant la largeur et l'épaisseur des éprouvettes.
Pour mesurer l'anisotropie, on utilise un coefficient r
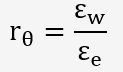
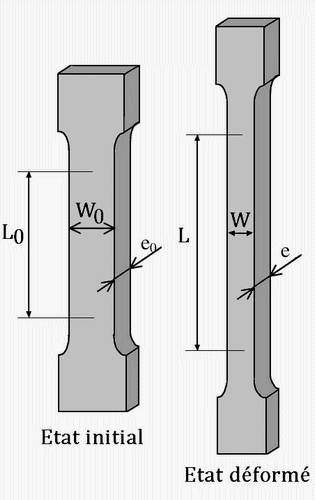
ε
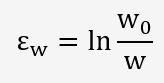
ε
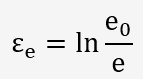
d'où la formule du calcul du coefficient d'anisotropie:
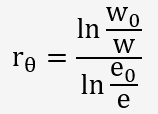
Les mesures peuvent être obtenues avec un double contractomètre.
Comme la mesure de la variation d'épaisseur est difficile, on effectue plutôt la mesure d'allongement:
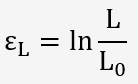
Puisque le volume de l'éprouvette reste constant pendant la déformation plastique, on peut calculer la déformation en épaisseur par simple différence:
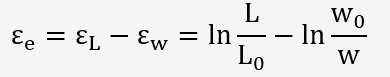
d'où la formule du calcul du coefficient d'anisotropie:
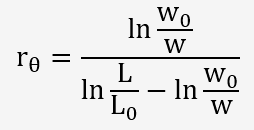
Les mesures sont alors obtenues avec un extensomètre combiné avec un contractomètre.
Il suffit d'arrêter l'essai de traction dans la zone d'allongement homogène avant la striction, un allongement de 20% est habituellement utilisé pour les aciers doux.
La valeur de r
On peut donc définir une valeur moyenne du coefficient en faisant l'essai selon plusieurs directions, la formule la plus courante est la suivante:
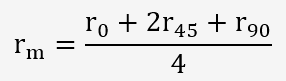
0, 45 et 90 représentent les angles en degré par rapport à la direction de laminage.
Ce coefficient est utilisé pour caractériser l'aptitude à l'emboutissage des tôles minces et il peut être mesuré à froid comme à chaud.
Les principales normes les plus utilisées:
ISO 6892-1: Matériaux métalliques - Essai de
traction - Partie 1 : Méthode d'essai à température ambiante
ISO 6892-2: Matériaux métalliques - Essai de traction - Partie
2 : Méthode d'essai à température élevée
ASTM E8/E8M: Standard Test Methods for Tension Testing of Metallic Materials
ASTM E21: Standard Test Methods for Elevated Temperature Tension Tests of
Metallic Materials
ASTM E 370: Standard Test Methods and Definitions for Mechanical Testing of
Steel Products
