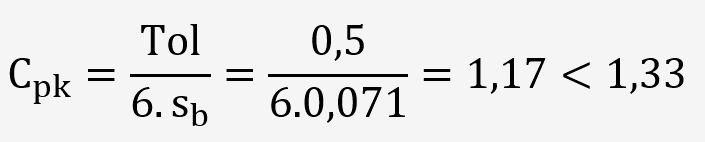Constat:
Une entreprise répond à un appel d'offre, il s'agit de réaliser des pièces forgées en acier répondant à un cahier des charges précis.
La première question que s'est posée le patron avant même d'établir un prix, c'est: "est-ce que mon process de forge me permet de répondre au cahier des charges du client".
Le plan lui donne une tolérance générale sur les surfaces brutes largement atteignable mais une côte avec une tolérance spécifique est nettement plus serrée et c'est elle qui pose un problème.
Les pièces seront livrées pas série de 13 pièces (1 pièce pour essai de prémontage par le client et 12 pièces pour montage définitif si l'essai est concluant).
Principe:
Le bureau d'étude se penche sur la question et il ressort que l'entreprise ne connait pas son coefficient de capabilité.
Ce dernier est estimé par la relation suivante:

En fait, cette formule intéresse l'entreprise dans une autre présentation :
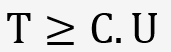
L’exigence client (tolérance spécifique
du plan) doit être supérieure au coefficient de capabilité
multiplié par l'incertitude de mesure.
La norme NF EN ISO 14253-1 propose un coefficient de capabilité (C
= 8, ce coefficient est contractuel et doit être négocié
avec le client) pour une incertitude exprimée avec un niveau de confiance
de 95% (k = 2).
Le coefficient implicite de l’entreprise peut être
évalué en connaissant la tolérance moyenne habituellement
vérifiée et l’incertitude moyenne du processus de contrôle.
Il faut rappeler que l’incertitude sur une donnée est tout aussi
importante que la donnée elle-même, puisqu’elle décide
de la fiabilité que l’on peut accorder à cette dernière
et, par voie de conséquence, de la fiabilité à accorder
au process reposant sur ce résultat.
Cette incertitude globale de mesure est la somme de plusieurs facteurs :
- La capabilité du process de fabrication (toutes étapes confondues)
qui est intégrée à l’incertitude pièces
lors des mesures.
- L’incertitude des instruments de mesures
- L’incertitude des opérateurs
L’acceptation de tout contrat devrait être associée à
cette démarche, certaines côtes trop restrictives en fabrication
se traduisent par une prise de risque sur la mesure et par conséquent
sur la conformité du produit.
Application numérique:
Le plan mentionne la tolérance suivante:
![]()
Les 13 pièces sont fabriquée par un seul opérateur pour réduire la dispersion.
L'écart-type d'une présérie après mesurage est de : 0,071 mm.
L'incertitude de répétabilité est donnée par le relation suivante:
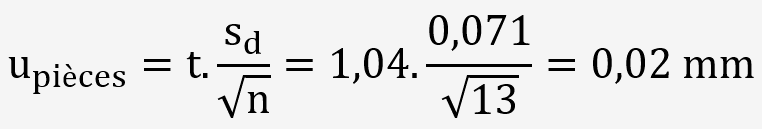
t: coefficient de Student qui vaut 1,04 pour un degré de liberté (n-1=12).
L'incertitude de l'opérateur est estimée à la résolution du pied à coulisse soit 10 µm et suit une distribution rectangulaire.
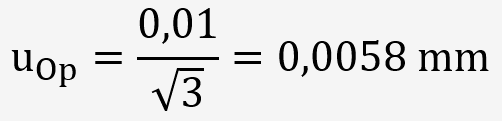
L'incertitude de l'équipement de mesure est donnée par le certificat du pied à coulisse: 18 µm et suit une loi normale.
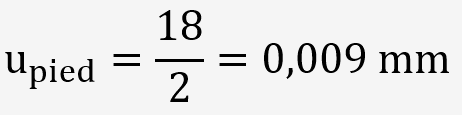
L'incertitude globale U est donné par la moyenne quadratique des différentes composantes:
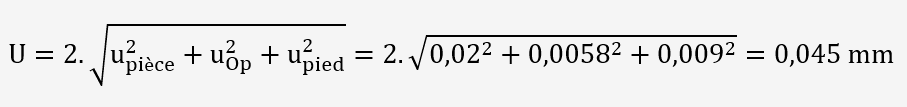
L'entreprise peut en déduire son coefficient de capabilité:
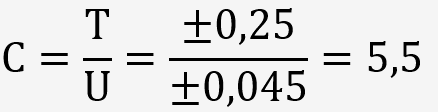
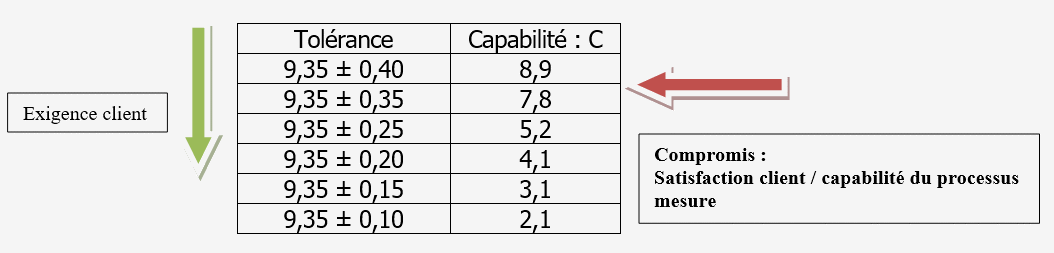
La difficulté réside sur la connaissance de
la capabilité du processus pour une pièce donnée.
Pour une capabilité C = 8, la côte de 9,35 mm aurait dû
avoir une tolérance de ±0,36 mm ou en conservant la tolérance
client, une incertitude de ±0,031 mm or l’incertitude opérateur
et celle du pied à coulisse restant identiques, par conséquent:
Upièce = 0,0069 mm (valeurs maxi/mini comprises entre 9,33 et 9,37
mm) d'ou des rebuts plus importants ou l'impossibilité pour l'entreprise
de prendre le marché avec ses moyens actuels.
Le calcul du Cpk montre effectivement que le process n'est pas capable de réaliser les pièces: