Approche bayésienne et incertitude de mesure

L'approche est très souvent éloignée d'une vision pragmatique pour le laborantin, les démonstrations s'appuient sur pléthore de formules théoriques qui n'invitent pas à la découverte de ce concept d’inférence bayésienne qui est régulièrement réservée à un traitement statistique de données volumineuses par des logiciels dédiés (calculs d'intégrales).

L'inférence statistique est l'ensemble des méthodes permettant d'induire à partir de groupe réduit de données (échantillonnage), les caractéristiques d'un groupe général (population), en fournissant une mesure de la certitude de la prédiction : la probabilité d'erreur.

elle nécessite:
- La connaissance antérieure des résultats intégrée dans le calcul de la probabilité,
- Lors de l’acquisition d’une nouvelle donnée, l’hypothèse est évaluée suivant ce niveau de connaissance antérieure,
- La méthode de calcul est itérative, c’est-à-dire que, à chaque nouvelle information, le calcul est révisé et les résultats réévalués, toujours en fonction de ce niveau de connaissance antérieure.

Nous allons essayer d'appliquer ce concept au travers d'un exemple pratique à un niveau accessible par le laborantin, l'objectif n'étant pas de faire un cours de mathématiques même si elle sont nécessaires, ni de statistiques mais simplement de faire comprendre les données d'entrées nécessaires et l'objectif de sortie.

Ce concept devrait se généraliser dans les années à venir grâce à l'IA, les exigences de temporalité (vérification annuelle, vérifications périodiques,...) pourront être augmentées sur la base d'une justification technique et suite à la détermination de la probabilité d'obtenir un résultat conforme au regard des résultats précédents.

Différence entre une approche "Fréquentiste: GUM " et "Bayesienne"
	Fréquentiste	Bayesienne
Paramètre du modèle	Fixé et constantes inconnues Pas de déclaration probabilistique	Variables aléatoires (détermination non exacte, incertitude en terme de probabilité ou de distribution)
Probabilité	Objective, fréquence relative	Subjective, degré de croyance
Principaux résultats	Estimation ponctuelle avec erreur type	Probabilité à postériori
Estimation / Inférence	Utiliser les données pour estimer au mieux les paramètres inconnus	Utiliser une valeur sur son étendue de variabilité aussi proche que possible en utilisant les données à jour. Utilisation d'une méthode de simulation: générer des données à postériori et les utiliser pour estimer les valeurs d'intérêt.
Estimation de l'intervalle	Intervalle de confiance : affirmation qu'il englobe la vraie valeur et reflète l'incertitude: par exemple (95%)	Intervalle crédible: affirmation selon laquelle la vraie valeur se trouve à l'intérieur de la probabilité mesurable, déclaration de probabilité directe sur les paramètres.

 

Le théorème de Bayes:

Il s’écrit de la façon suivante :

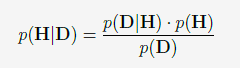
avec:

- p(H/D) = probabilité de l'hypothèse H au regard du processus D (degré de confiance à postériori en fonction de toutes les données disponibles)

- p(D/H) = fonction de vraisemblance des données du processus D au regard de l'hypothèse H (dans le cadre d'un processus normalement aléatoire)

- p(H) = probabilité "à priori" que l'hypothèse H soit vérifiée (conviction, estimation, calcul,...)

- p(D) = probabilité "a priori" (ou marginale) de D.

Cette forme discrète du théorème de Bayes est rarement utilisée dans l'analyse de l'incertitude de mesure.

À la place, c'est la forme continue du théorème de Bayes qui est généralement utilisée.

Pour un problème à une dimension (c'est-à-dire un paramètre inconnu A), la forme continue traditionnelle (et actuelle) du théorème de Bayes s'écrit :

A étant représenté par son espérance mathématique µ et son écart-type σ.

Problème:

1.0/ Donnée d'entrées:

Supposons que nous effectuons un essai de traction sur un matériau pour déterminer sa résistance à la rupture.

Nous avons effectué plusieurs mesures (n=5) de la contrainte à la rupture et nous souhaitons estimer l'incertitude de cette mesure en utilisant une approche bayésienne.

 

n	1	2	3	4	5
Résultats (MPa)	502	498	500	503	499

 

 

Nous allons déterminer la moyenne et l'écart-type des 5 résultats:

n = 5	Moyenne (MPa)	Ecart-type (MPa)
	500,4	SD=2,07

 

Méthode bayésienne modifiée avec approche fréquentiste

2.1/ Facteur de correction de biais:

Le biais dans les estimations statistiques peut survenir pour diverses raisons, notamment en raison de la taille limitée de l'échantillon ou de la nature des données.

Le facteur de correction de biais c4 est une technique utilisée pour ajuster les estimations afin de les rendre plus précises.

Points clés concernant c4 :

Objectif: Réduire le biais dans les estimations des paramètres du modèle.
Application: Utilisé dans les modèles bayésiens pour améliorer la précision des estimations.
Calcul: Le calcul de c4 peut dépendre du modèle spécifique et des données disponibles. Il est souvent basé sur des techniques analytiques ou des simulations.

Dans le cas présent, on utilisera la distribution GAMMA:

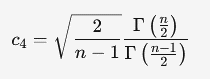
La fonction GAMMA Γ se calcul avec EXCEL: GAMMA(X) avec n = 5.

C4=0,94

2.2/ Calcul de l'incertitude élargie de type A (sans information a priori):

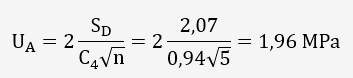
3.1 / Calcul de l'incertitude (avec information a priori):

Supposons que nous avons une information a priori sur la résistance à la rupture, représentée par une distribution normale avec une moyenne xA priori=500 MPa et un écart-type σA priori=2 MPa.

3.2/ Moyenne à postériori:

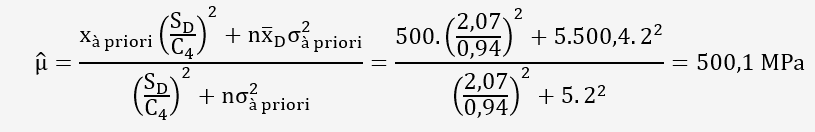
3.3/ Incertitude élargie à postériori:

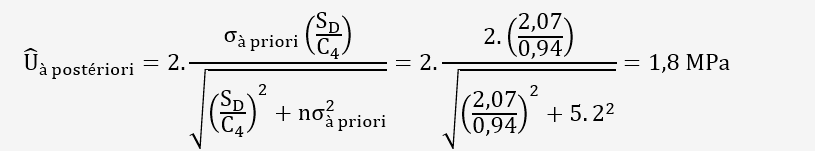
Méthode bayésienne traditionnelle

Nous avons les mêmes données de l'essai de traction :

4.1/ Choix de la distribution a priori:

Pour simplifier, nous choisissons une distribution a priori non informative, comme la distribution de Jeffreys, qui est souvent utilisée lorsqu'il n'y a pas d'information a priori spécifique et qui est:

Non-informative : La distribution de Jeffreys est conçue pour être non informative, ce qui signifie qu'elle ne favorise aucune valeur particulière du paramètre. Elle est souvent utilisée lorsque l'on n'a pas d'information a priori sur le paramètre.

Invariance : Une propriété importante de la distribution de Jeffreys est son invariance sous les transformations de paramètres. Cela signifie que si vous changez la paramétrisation du modèle, la distribution de Jeffreys reste la même.

Calcul : La distribution de Jeffreys est proportionnelle à la racine carrée du déterminant de l'information de Fisher.

Pour un paramètre A, la densité de Jeffreys est donnée par :

avec I(A) est l'information de Fischer pour le paramètre A

L'information de Fisher est définie comme la variance de la dérivée du logarithme de la fonction de vraisemblance par rapport au paramètre d'intérêt.

Elle quantifie la courbure de la fonction de vraisemblance autour de son maximum.

Une grande quantité d'information de Fisher signifie que l'échantillon fournit une estimation fiable du paramètre.

Applications : Elle est souvent utilisée dans les analyses bayésiennes lorsque l'on souhaite que les résultats soient principalement influencés par les données observées plutôt que par les croyances a priori.

Pour un paramètre de moyenne µ avec un écart-type σ, la distribution de Jeffreys est :

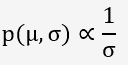
4.2/ Calcul de la vraisemblance:

La vraisemblance des données observées, supposant que les erreurs de mesure suivent une distribution normale, est donnée par :

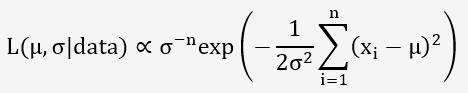
4.3/ Application de la règle de Bayes:

La distribution à priori est obtenue en combinant la distribution a priori avec la vraisemblance :

En substituant les expressions, nous obtenons :

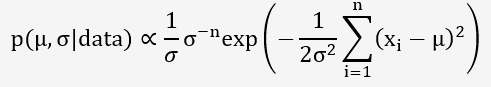
Pour obtenir la distribution à postériori de µ, nous devons intégrer sur σ. Cependant, cette intégration est complexe et nécessite souvent des méthodes numériques comme Monte Carlo.

4.4/ Calcul de l'incertitude élargie de type A (a priori non informative):

Pour simplifier, nous pouvons utiliser une approximation en supposant que la distribution postérieure de µ suit une distribution normale avec une moyenne x¯D et un écart-type ajusté.

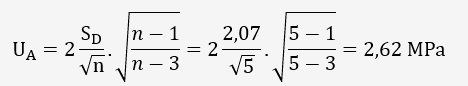
En utilisant la méthode bayésienne traditionnelle avec une distribution a priori non informative, nous avons estimé l'incertitude de la résistance à la rupture.

Cette approche montre comment les données observées mettent à jour notre croyance initiale sur la distribution des paramètres, en utilisant la règle de Bayes.

L'incertitude obtenue est différente de celle obtenue par la méthode bayésienne modifiée, ce qui illustre les différences entre les approches fréquentistes et bayésiennes traditionnelles.