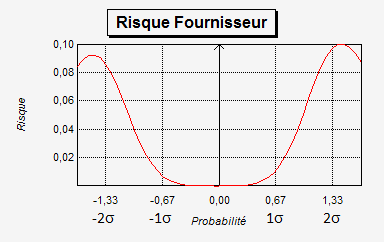
Ces estimations font souvent appel à des notions mathématiques compliquées et sont la plupart du temps, abordées avec une présentation complexe (très théorique avec des intégrales), sans aucune application numérique pour expliquer la démarche de calcul, ce qui rebute la plupart des lecteurs qui ont oubliés leurs connaissances mathématiques et de surcroit les néophites qui s'intéressent à ces notions (par curiosité ou par obligation pour aborder les nouveautés de la norme ISO 17025).
Nous allons essayer de rendre plus accessible ces notions par des applications numériques.
![]()
Risque du client: probabilité pour que le résultat d'un essai ou d'une analyse accepté par votre client soit en réalité non-conforme.
Ce risque est appelé: β et est noté probabilité
P
Risque de l'OEC (producteur du résultat): probabilité pour que le résultat d'un essai ou d'une analyse déclaré non-conforme soit en réalité conforme.
Ce risque est appelé:α et est noté probabilité
P
![]()
Reprenons nos 10 mesurages de pH: voir Régles de décision
| 10,2 |
9,7 |
10,3 |
10,1 |
9,8 |
10,5 |
10,0 |
9,6 |
10,4 |
9,5 |
Nous connaissons les bornes Maxi et Mini, l'écart-type: σ=0,348 et l'espérance mathématique: µ qui n'est autre que la moyenne: 10,01.
La probabilité d'obtenir des valeurs conformes est donnée par la relation suivante:
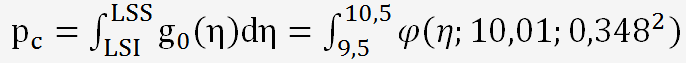
avec: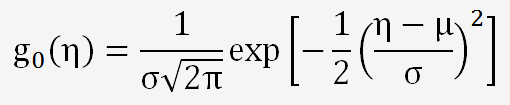
Loi supposée normale de la distribution (η représente la valeur du pH)
Le calcul de cette intégrale revient à calculer la surface de la gaussienne bornée par les limites fixées par le client:
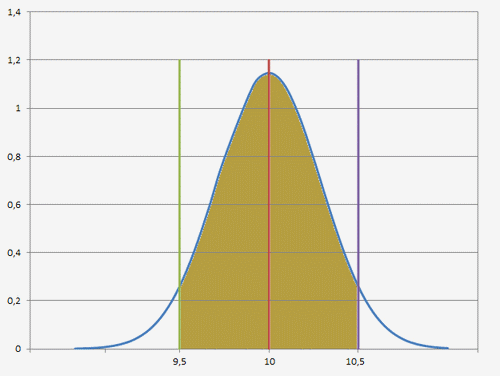
Surface bornée entre [9,5 et 10,5].
La fonction EXCEL suivante permet de déterminer cette surface: =[LOI.NORMALE(10,5;10,01;0,348;VRAI)-LOI.NORMALE(9,5;10,01;0,348;VRAI)]=0,85 soit Pc=85%.
Attention, la distribution doit être cumulative ("VRAI").
Le risque client Rc=1-Pc est la différence entre 100% et la probabilité d'obtenir des analyses conformes: 85% soit 15%.
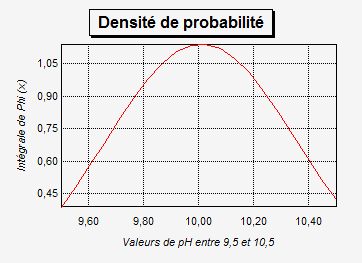
![]()
En supposant que mon client souhaite un risque Rc=10%, il faut donc que mon Pc soit de 90%, j'ai trois possibilités pour atteindre cet objectif:
1) Augmenter les bornes (en accord avec le client)
2) Utiliser un dispositif de mesurage plus précis (décision interne)
3) Garder le même équipement, diminuer les bornes et prendre en compte l'incertitude (décision interne).
Connaissant l'écart-type de la série de mesures, on peut déterminer une incertitude de type A (estimée sur la répétabilité des mesurages):
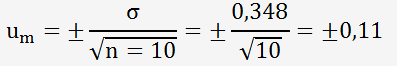
En supposant que je prenne une bande de garde équivalent à l'incertitude élargie en supposant une loi normale (k=2), cela revient à situer mes bornes à: [9,3 et 10,7].
En recalculant la surface de la gaussienne: =[LOI.NORMALE(10,7;10,01;0,348;VRAI)-LOI.NORMALE(9,3;10,01;0,348;VRAI)]=0,95 soit Pc=95%.
Le risque client Rc=1-Pc est la différence entre 100% et la probabilité d'obtenir des analyses conformes: 95% soit 5%, l'objectif est atteint.
![]()
L'équipement de mesure (Titrimètre) était équipé d'une burette de 20 ml, je la remplace par une burette de 5 ml permettant des incréments beaucoup plus précis.
L'électrode de pH basique est remplacée par une électrode dite de "qualité supérieure", permettant d'apprécier 2 chiffres après la virgule et calibrée en trois points.
Mon titrant (soude) fabriqué "in house" est acheté dans le commerce en tant que solution certifiée et associée à une incertitude.
Reprenons les valeurs obtenues après 10 nouveaux titrages:
| 10,16 |
9,72 |
10,25 |
10,04 |
9,84 |
10,47 |
10,00 |
9,65 |
10,36 |
9,59 |
Nous connaissons les bornes Maxi et Mini, l'écart-type: σ=0,304 et l'espérance mathématique: µ qui n'est autre que la moyenne: 10,00.
La fonction EXCEL suivante permet de déterminer cette différence: =[LOI.NORMALE(10,5;10,00;0,304;VRAI)-LOI.NORMALE(9,5;10,00;0,304;VRAI)]=0,90 soit Pc=90%.
Le risque client Rc=1-Pc est la différence entre 100% et la probabilité d'obtenir des analyses conformes: 90%, soit 10%, l'objectif est atteint.
![]()
Hypothèse de base: la série de mesurage suit une loi normale (dans
le cas contraire, la fonction φ
| 10,2 |
9,7 |
10,3 |
10,1 |
9,8 |
10,5 |
10,0 |
9,6 |
10,4 |
9,5 |
La moyenne est y
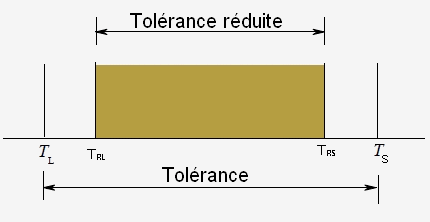
Les bornes sont réduites d'une bande de garde équivalent à
la moitié de l'incertitude soit [T
La zone de tolérance du client est [T
L'étendue de la plage réduite w=10,44-9,56=0,88 = 4U
Le risque client est donné par la relation suivante:
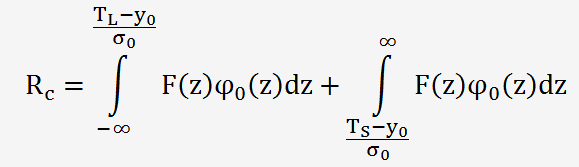
La fonction φ
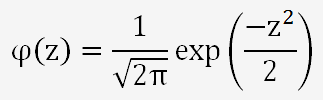
F(z) est une fonction de probabilité qui s'exprime par:
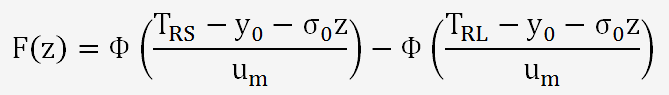
Et enfin, le risque de l'OEC (producteur) s'exprime par la relation suivante:
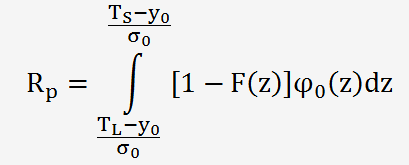
Déterminons la fonction F(z): les valeurs obtenues correspondent aux données sans arrondissage.
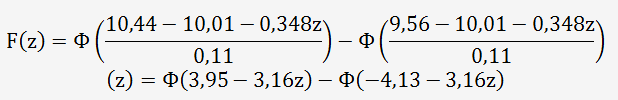
Déterminons z que l'on nommera z
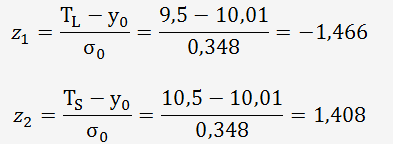
Ce type de fonction ne se résoud pas manuellement et nécessite généralement de nombreuses intégrations numériques ou par la méthode de Monté-Carlo.
Il existe des logiciels ou des applications WEB qui peuvent vous aider à résoudre ce type de calcul.
Nous allons déterminer R
En fait, compte tenu de la tolérance et de notre incertitude, il n'y a pas d'intérêt de borner entre - ∞ et ∞, d'autant que les softs ou les applications n'intégrent pas réellement les fonctions mais appliquent ce que l'on appelle la "méthode des trapèzes", ils fractionnent la courbe en petites surfaces bornées qu'il faudra sommer et considèrent que la courbe sur ces petites portions est assimilable à une droite, plus le fractionnement est important, meilleure est l'approximation.
Le risque client R
Le risque fournisseur (OEC) borné entre [-1,465;1,408] donne 0,086 soit 8,6% pour une probabilité de 95%, ce qui est parfaitement acceptable.
Vous trouverez le calcul détaillé de cet exemple en utilisant EXCEL et une méthode mathématique "Calcul des risques Clients et Fournisseurs avec EXCEL" pour vous affranchir du calcul d'intégrale qui n'est pas réalisable sous EXCEL, l'application Windows ne pouvant pas réitérer les bornes de l'intégrale.