Les limites des cartes de contrôle
Il y-a des bonnes et une mauvaise façon de calculer les limites de cartes de contrôle.
Connaissez-vous leurs différences?
Anecdote:
Nous sommes en 1930, un grand patron demande à son
chef d'équipe Paul, d'utiliser une carte de contrôle pour surveiller
la production de l'usine.
Paul ne savait pas par où commencer, alors il s'est demandé
quelles sont les données qu'il devait collecter et après réflexion,
il sait dit qu'il pourrait commencer par les données qui sont déjà
connues dans l'usine.
Paul commence donc sa collecte avec une feuille de journal sur laquelle il
note la production de la semaine précédente.
Sur la feuille de journal, il écrit le poids de chaque lot fabriqué
par les opérateurs en production.
Paul trace les poids des lots sur un morceau de papier millimétré
et après avoir rempli la première page, il calcule les limites
d'un tableau de valeurs individuelles, aussi connu comme un tableau Xmr (valeur
individuelle X et étendue mobile mR).
Bien sûr, le processus est hors de contrôle et imprévisible.
Même si chaque lot a été pesé, et même si les opérateurs ont écrit chacun de ces poids, le tableau ne peut pas leur permettre de produire des lots avec des poids constants. Les poids imprévisibles signifiaient que la formulation était en train de changer de manière imprévisible et cela se traduisait par un sentiment de fatalisme car quelques jours auparavant les poids avaient été mieux que d'autres et il ne pouvait rien faire pour y remédier.
Comment Paul pouvait-il déterminer que le processus était imprévisible? La réponse se trouve dans la façon dont les limites sont calculées. Nous allons voir comment Paul a fait ses calculs.
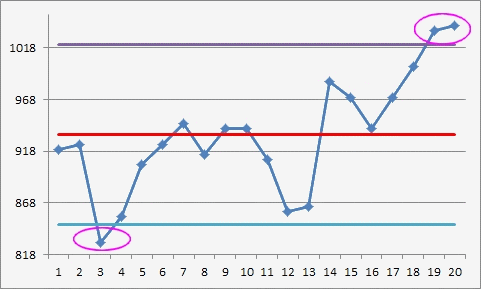
Ci-dessous les résultats de la production en kg sur 20 jours
| 920 |
925 |
830 |
855 |
905 |
| 925 |
945 |
915 |
940 |
940 |
| 910 |
860 |
865 |
985 |
970 |
| 940 |
970 |
1000 |
1035 |
1040 |
La première étape consiste à déterminer la ligne centrale de la carte, qui est généralement la moyenne des valeurs individuelles. Pour ces 20 valeurs, la moyenne est de 934.
Il existe deux méthodes pour calculer les limites
de la carte de contrôle Xmr, après la détermination de
la ligne centrale, Paul calcule les plages mobiles.
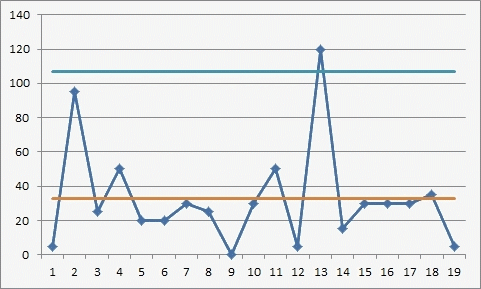
Les plages mobiles sont les différences entre les valeurs successives.
Pour la première paire de données de la plage, l'étendue est de 925 à 920 = 5.
La deuxième paire est de 830 à 925 = -95. Cependant, par convention, les plages mobiles sont toujours positives, Paul laisse tomber le signe négatif et obtient donc une plage mobile de 95. Pour les 20 données ci-dessus, les 19 plages mobiles sont les suivantes:
| / |
5 |
95 |
25 |
50 |
| 20 |
20 |
30 |
25 |
0 |
| 30 |
50 |
5 |
120 |
15 |
| 30 |
30 |
30 |
35 |
5 |
Avec une ligne centrale et un ensemble de plages mobiles, Paul est maintenant prêt à calculer les limites en utilisant une des deux méthodes.
Une première méthode correcte:
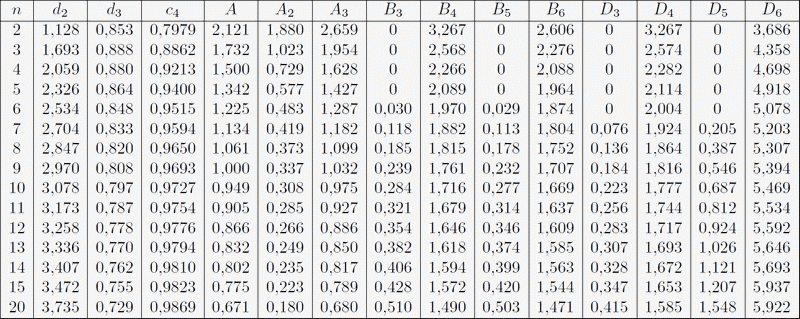
Voir le tableau des constantes de Burr en bas de page.
La méthode la plus courante pour déterminer les limites pour les cartes Xmr est d'utiliser les étendues mobiles moyennes, ce qui est communément désigné par le symbole: Rbar
Les limites de la carte sont déterminées en
multipliant l'étendue mobile moyenne (32,63) par la
constante A
Xbar-2,66Rbar et Xbar+2,66Rbar avec 2,66Rbar=32,63x2,66=86,8 soit Limite basse = 847,2 et Limite Haute = 1020,8
La limite supérieure pour le graphique des étendues
est obtenue en multipliant l'étendue mobile moyenne par la constante
3,267 (D
Une seconde méthode correcte:
Elle consiste à calculer les limites de la carte de contrôle pour un tableau de valeurs individuelles en utilisant l'étendue mobile médiane (25) pour les 19 valeurs, pour déterminer la médiane d'un ensemble de valeurs, il suffit d'ordonner les valeurs en une liste croissante et de choisir la valeur qui est au centre de cette liste, ce qui est communément désigné par le symbole:
![]()
Les limites de la carte peuvent être trouvées en multipliant l'étendue mobile médiane par la constante 3,145 puis en ajoutant et en soustrayant de ce produit à partir de la moyenne.
En multipliant:
![]() .=
25 par la constante 3,145, cela donne 78,625, et les limites de la carte sont
donc:
.=
25 par la constante 3,145, cela donne 78,625, et les limites de la carte sont
donc:
Xbar-78,625 et Xbar+78,625 soit Limite basse = 855,4 et Limite Haute = 1012,6
La limite supérieure pour le graphique des étendues est obtenue en multipliant l'étendue mobile médiane par la constante 3,865. Pour ces données, cette limite est de 96,6 = 3,865 x 25.
Ces limites sont légèrement plus étroites
que celles calculées par la première méthode, et maintenant,
la carte aura un quatrième point à l'extérieur des limites
(la valeur 855).
Il n'y a pas de différence pratique entre ces deux méthodes
de calcul des limites.
Une méthode incorrecte:
Cette méthode ne doit être utilisée que lorsque la dispersion est maîtrisée et encadrée.
Une méthode commune, mais erronée pour le calcul des limites d'une carte de contrôle est d'utiliser une mesure de la dispersion, qui est calculée à partir de toutes les données. Par exemple, les 20 données pourraient donner un écart type calculé. Le symbole commun pour cette statistique est la lettre minuscule s. Pour ces 20 données:
s = 56,5
Les limites à Trois-Sigma sont alors calculées à tort comme (moyenne + Trois Sigma):
934 ± 170 soit Limite basse = 764 et Limite haute = 1104
L'utilisation des méthodes appropriées pour calculer les limites
permet de détecter les alertes dans les données, en dépit
du fait que nous avons utilisés les données contenant des alertes
dans nos calculs. Les méthodes correctes sont toujours basées
sur un chiffre moyen ou une dispersion médiane.
Les méthodes incorrectes vont inévitablement conduire à
limiter les alertes qui sont présentes dans les données, et
donc masquer les problèmes.
Les méthodes incorrectes ont tendance à se baser sur une seule
mesure de dispersion, qui a été calculée en utilisant
toutes les données.
Si vous souhaitez utiliser un écart-type, reportez vous à la fiche: "Choisir les bornes dans les cartes de contrôle"