Choisir les bornes dans les cartes de contrôle
Les cartes de contrôle sont largement utilisées par les laboratoires pour surveiller une caractéristique qui permet d'assurer que l'essai ou l'analyse est toujours fiable. Monsieur Walter A. Shewhart a introduit le concept des cartes de contrôle dans les années 1920.
En fait, plusieurs cartes de contrôle peuvent être élaborées
pour surveiller des observations individuelles ou des groupes de données
et ces différents types de cartes permettent d'anticiper les changements
ou les tendances des caractéristiques concernées.
Les cartes pour les données de variables et les données d'attributs,
comprennent les éléments suivants:
Carte de contrôle avec moyenne x̄ et R (différence entre Maxi et Mini pour chaque série de donnée: étendue mobile).
Carte de contrôle avec moyenne x̄ et s (écart-type des données).
Carte de contrôle individuelle (très peu de mesures).
Carte de contrôle aux attributs (par exemple: fraction de non-conformes "p", Nombre de non-conformes "nP", surveillance des non-conformités "c", surveillance de la moyenne des non-conformités "u").
Pour chacune de ces cartes de contrôle, les hypothèses de distribution doivent être satisfaites:
- Les données suivent une distribution normale (si la normalité
n'est pas démontrée, les performances globales de ces cartes
peuvent être très médiocres et entraîner des avertissements
erronés).
- Les limites de contrôle sont calculées sur la base des données
du processus et lors du calcul des limites de contrôle, il est nécessaire
de collecter autant de données que possible (au moins 25 mesurages).
- Il est souhaitable que la taille de l'échantillon soit maintenue aussi constante si possible.
Reprenons tous ces exemples avec une application numérique:
Carte de contrôle avec moyenne x̄ et R
Supposons qu'un laboratoire veuille vérifier à chaque jour
d'utilisation, que son équipement soit conforme, pour cela il réalise
n=3 mesurages X
| Jours |
1 |
2 |
3 |
Moyenne | Max - Min = R | ||
| 1 | 9,7 |
10,3 |
10,1 |
10,0 | 0,6 | ||
| 2 | 9,8 |
10,2 |
10,5 |
10,2 | 0,7 | ||
| 3 | 10,2 |
10,3 |
10,1 |
10,2 | 0,2 | ||
| 4 | 10,4 |
10,3 |
10,0 |
10,2 | 0,4 | ||
| 5 | 9,7 |
10,5 |
10,2 |
10,1 | 0,8 | ||
| 10,2 | 0,54 | ||||||
Il détermine les limites de sa carte de contrôle qui seront dynamiques en fonction des résultats répétés:


Carte de contrôle avec moyenne x̄ et s
Dans la mesure du possible, l'écart type de l'échantillon doit être utilisé lorsque la taille de l'échantillon n est grande, disons n> 10.
| Jours |
1 |
2 |
3 |
Moyenne | s | ||
| 1 | 9,7 |
10,3 |
10,1 |
10,0 | 0,31 | ||
| 2 | 9,8 |
10,2 |
10,5 |
10,2 | 0,35 | ||
| 3 | 10,2 |
10,3 |
10,1 |
10,2 | 0,10 | ||
| 4 | 10,4 |
10,3 |
10,0 |
10,2 | 0,21 | ||
| 5 | 9,7 |
10,5 |
10,2 |
10,1 | 0,40 | ||
| 10,2 | 0,27 | ||||||
Il détermine les limites de sa carte de contrôle qui seront dynamique en fonction des résultats répétés:


Carte de contrôle individuelle
Il existe de nombreuses applications pratiques dans lesquelles le mesurage ne consiste qu'en une seule observation (n = 1).
Cet état de fait peut provenir de processus très lents ou des processus dans lesquels la mesure est très onéreuse, comme avec des tests destructifs.
Une carte de contrôle individuelle pour les données variables
est appropriée pour ce type de situation.
La carte de contrôle individuelle utilise la plage mobile de deux sous-groupes
successifs ou deux jours consécutifs (=m) pour estimer la variabilité
du processus.
La plage mobile est donnée par:
![]()
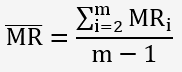
| Jours
|
Plage mobile = MR | |||
| 1 | 9,7 |
0 | ||
| 2 | 9,8 |
0,1 | ||
| 3 | 10,2 |
0,4 | ||
| 4 | 10,4 |
0,2 | ||
| 5 | 9,7 |
0,7 | ||
| m=5 | 10,0 | 0,35 | ||
Il détermine les limites de sa carte de contrôle qui seront dynamique en fonction des résultats répétés:
Par défaut, n'ayant qu'une valeur pour chaque jour, on prendra n = 2.


Carte de contrôle aux attributs
Les cartes de contrôle aux attributs sont utilisées pour les données discrètes ou de comptage.
La caractéristique intéressante est simplement une classification
de la mesure en une seule catégorie. Par exemple, les produits manufacturés
peuvent être mesurés mais classés uniquement comme défectueux
/ non défectueux, conformes / non-conformes ou réussis / échoués.
D'autres situations peuvent impliquer la surveillance du nombre de non-conformités
sur un produit afin de détecter des erreurs telles qu'un nom incorrect,
des informations manquantes ou erronées ou des services non identifiés.
Les cartes de contrôle des variables ne conviennent pas à toutes
les situations.
Lorsque la variable d'intérêt ou la caractéristique est
le nombre de non-conformités par unité, les cartes "p"
et "np" ne sont pas appropriées.
La carte de contrôle "p": fraction de non-conformes
La caractéristique qui nous intéresse peut être placée dans l'une des deux catégories suivantes: réussies / échouées, conformes / non conformes, etc.
Pour simplifier, le terme «non-conforme» sera utilisé comme référence générale quelles que soient les catégories finales à utiliser.
La notation à utiliser est la suivante:
• n: nombre de produits examinés (taille du lot, taille de l'échantillonnage).
• m: nombre de sous-groupes.
• X: nombre de produits non-conformes trouvés dans l'échantillonnage
de taille n, où X ≤ n.
• p: probabilité que la caractéristique ne soit pas conforme.
Ce paramètre est souvent inconnu et doit être estimé.
• p̂: fraction d'échantillon non-conforme.
Par définition, cette probabilité est données par la relation:
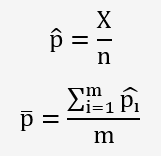
| Jours
|
n | X: non conforme | ||
| 1 | 100 |
8 | 0,08 | |
| 2 | 98 |
7 | 0,07 | |
| 3 | 104 |
6 | 0,06 | |
| 4 | 99 |
4 | 0,04 | |
| 5 | 97 |
5 | 0,05 | |
| m=5 | Estimateur de n = 99,6 | 0,06 | ||
Si la taille du lot est identique (100 par exemple), utiliser n=100 tel quel, si elle est différente comme dans l'exemple ci-dessus, prendre la moyenne comme estimateur de n, ce qui est plus facile que de définir des limites différentes pour chaque famille de lots identiques.

La limite basse LCL sera forcée à 0 "zéro" si elle est négative.
La carte de contrôle "np": nombre de non-conformes
La carte de contrôle "np" est une variante de la carte" p", le nombre réel de produits non conformes étant représenté sur la carte.
La carte "np" et la carte "p" pour le même problème fourniront des informations identiques. Autrement dit, si la carte "p" indique qu'un processus est hors de contrôle, alors la carte "np" indiquera également que ce même processus est hors de contrôle.
L'une des raisons pour lesquelles la carte np est une alternative intéressante à la carte "p" est sa facilité d'interprétation (valeur absolue).
Pour la carte "np", la fraction moyenne de non-conforme peut être calculée comme suit:
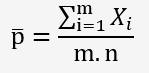
| Jours
|
n | X: non conforme | ||
| 1 | 100 |
8 | 0,08 | |
| 2 | 98 |
7 | 0,07 | |
| 3 | 104 |
6 | 0,06 | |
| 4 | 99 |
4 | 0,04 | |
| 5 | 97 |
5 | 0,05 | |
| m=5 | Estimateur de n = 99,6 | 0,06 | ||

On peut remarquer que les limites de la carte "np" sont proportionnelles à la carte "p" avec un facteur = n.
La limite basse LCL sera forcée à 0 "zéro" si elle est négative.
La carte de contrôle "c" pour la surveillance des non-conformités
Si la taille du sous-groupe n est constante d'un sous-groupe à l'autre, la carte "c" est une carte de contrôle appropriée pour les non-conformités.
Pour la carte "c", on distingue:
• n = nombre d'unités inspectées, taille de l'échantillon
(il peut s'agir d'une taille n = 1 ou supérieure)
• m = nombre de sous-groupes
• X = nombre de non-conformités par unité inspectée
ou par sous-groupe
• c = nombre moyen de non-conformités:
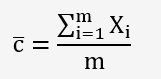
| Jours
|
n | X: non conforme |
| 1 | 100 |
8 |
| 2 | 100 |
7 |
| 3 | 100 |
6 |
| 4 | 100 |
4 |
| 5 | 100 |
5 |
| m=5 | 6 |

La limite basse LCL sera forcée à 0 "zéro" si elle est négative.
La carte de contrôle "u" pour la surveillance de la moyenne des non-conformités
Comme les cartes " p" et "np", les cartes
"c" et "u" pour une taille d'échantillon constante
fourniront des résultats identiques.
Il n'est pas nécessaire que la taille de l'échantillon soit
constante d'un sous-groupe à l'autre pour la carte u.
Soit u
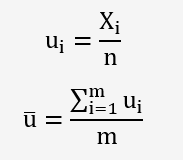
| Jours
|
n | X: non conforme | u |
| 1 | 100 |
8 | 0,08 |
| 2 | 100 |
7 | 0,07 |
| 3 | 100 |
6 | 0,06 |
| 4 | 100 |
4 | 0,04 |
| 5 | 100 |
5 | 0,05 |
| m=5 | 0,06 | ||
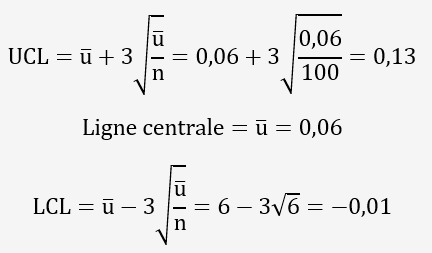
La limite basse LCL sera forcée à 0 "zéro" si elle est négative.
Limite d'utilisation
Les cartes de contrôle présentées s'appliquent généralement aux processus qui sont considérés comme des cycles longs et continus (par exemple, utilisation d'un MRC, 100 ou 200 fois).
Ces cartes ne conviennent pas pour les courts cycles de production ou de contrôle.
Les cartes de contrôle à court terme pour les données d'attribut sont en fait des cartes de contrôle standardisées.
L'attribut de la carte de contrôle de la caractéristique est normalisé et tracé sur une carte de contrôle.
Pour illustrer cela, considérons la valeur normalisée en utilisant le nombre de non-conformités (c.-à-d. la carte "c").
La valeur normalisée qui suit une distribution normale est:
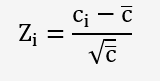
Avec les dispositions suivantes:
• Chaque point de donnée est normalisé
• La variable aléatoire standardisée Z
• La ligne centrale de toutes les cartes standardisées est zéro
• Les limites de contrôle pour toutes les cartes normalisées
sont –3 et 3
| Jours
|
n | X: non conforme | Z |
| 1 | 100 |
8 | 0,81 |
| 2 | 100 |
7 | 0,40 |
| 3 | 100 |
6 | 0,00 |
| 4 | 100 |
4 | -0,81 |
| 5 | 100 |
5 | -0,40 |
| m=5 | 6 | ||

Le processus est sous contrôle
![]()
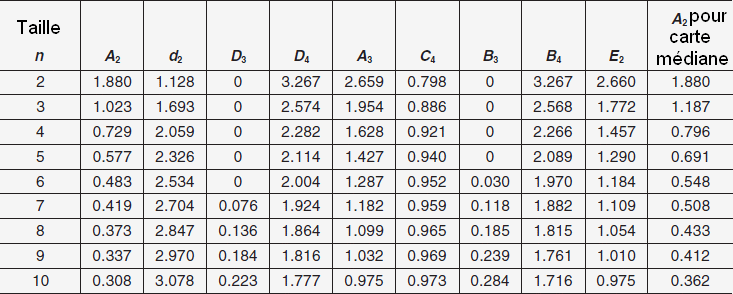
Constantes de Burr