Distribution gaussienne et probabilités

La grande majorité des technicien(ne)s de laboratoire réalise des analyses en répétant le processus plusieurs fois en espérant fournir à leurs clients un résultat qui soit le plus représentatif possible.

A ce résultat, l'opérateur va associer une incertitude de mesure élargie qui englobe tout le mesurande de l'essai, cette incertitude est généralement estimée pour une probabilité de 95 % avec un facteur d'élargissement K =2.

Lorsque l'opérateur réalise plusieurs mesures, il suppose que la distribution suit une loi normale, il calcule généralement un écart-type pour estimer la dispersion mais il se peut que la gaussienne ne soit pas symétrique par rapport à la moyenne.

Passons à une application pratique:

Un opérateur détermine la teneur en extrait sec d'une eau résiduaire: valeur attendue X%.

Après 10 étuvages d'un volume donné et stabilisation en dessiccateur, Il réalise N=10 pesages (résultats en gramme) et calcul un écart-type.

L'opérateur réitère ces pesées sur le même échantillon, il obtient donc une seconde série de 10 mesures:

Série	1	2	3	4	5	6	7	8	9	10	Moyenne	Ecart-type
1	9,5	9,0	9,0	12,3	13,0	9,0	13,0	9,0	13,0	9,0	10,6	1,9
2	9,0	12,5	9,3	13,0	12,9	9,1	13,0	9,0	9,5	12,7	11,0	1,9

Après une simple analyse visuelle, on ne peut que constater que les moyennes sont très proches et les deux écarts-types sont identiques, l'opérateur peut donc en toute "confiance" donner un résultat sur une des moyennes et une incertitude élargie de type A que l'on peut estimer de la manière suivante en faisant abstraction de l'erreur non significative de la balance et de la résolution de lecture:

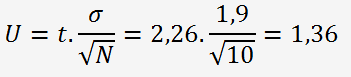
Avec t: coefficient de Student pour N-1 degrés de liberté (9): tableau G2 du GUM pour une probabilité de 95 %.

Quelles sont les différences entre ces deux séries de mesure:

Nous allons calculer le coefficient d'asymétrie SKEWNESS avec la relation suivante:

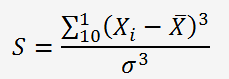
S1=3,6 et S2=0, on peut en conclure que la série1 présente une asymétrie positive (un plus grand nombre de valeurs se trouvent en dessous de la moyenne) et que la série 2 est parfaitement symétrique.

On peut également utliser EXCEL (=COEFFICIENT.ASYMETRIE(A1:A10)) mais la formule est différente:

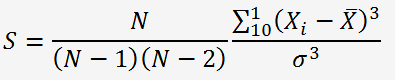
S1=0,5 et S2=0, la tendance est identique.

En connaissant cette tendance, pourrait-on définir une probabilité qui soit représentative des résultats obtenus:

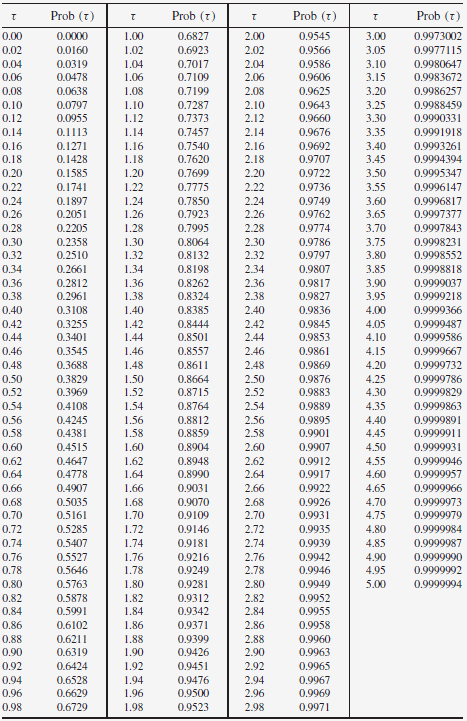
Nous allons déterminer les probabilités pour différentes situations:

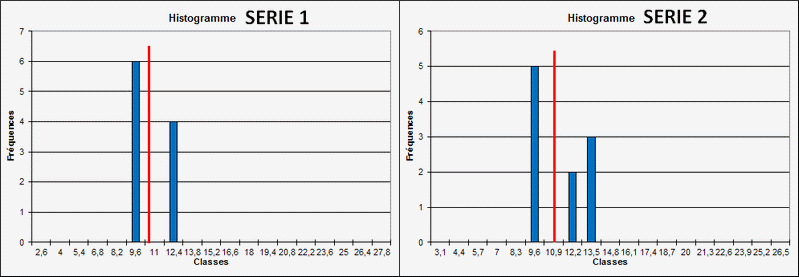
Série 1: la moyenne est de µ = 10,6 grammes et la répartition est asymétrique, les valeurs obtenues se trouvent sur la plage (9 à 13 grammes).

Calculons la probabilité d'obtenir des valeurs comprisent entre 9 et 10,6 grammes, pour cela on calcul la variable aléatoire définie par:

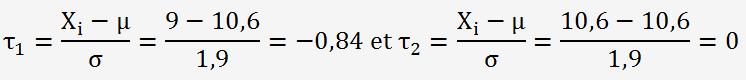
La probabilité Prob(9<Xi<10,6) est égale à ½Prob(-0,84)=½Prob(0,5991)≈30% (voir valeurs dans tableau ci-dessous)

 

Calculons la probabilité d'obtenir des valeurs comprisent entre 10,6 et 13 grammes, pour cela on calcul la variable aléatoire définie par:

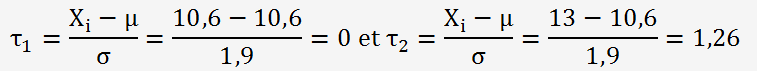
La probabilité Prob(10,6<Xi<13) est égale à ½Prob(1,26)=½Prob(0,7923)=½(79,2%)≈39,6%

Pour l'ensemble de la plage (9<Xi<13), la probabilité est égale à ½Prob(-0.84)+½Prob(1,26)=½(59,9%)+½(79,2%)≈69,6% (30,0+39,6)

Discussion: pourquoi avons nous plus de valeurs en dessous de la moyenne et la probabilité sur cette plage est inférieure à celle concernant les valeurs au dessus de la moyenne?

La réponse se trouve sur le choix de la plage, il ne faut pas perdre de vue que notre plage inférieure est égale (9-10,6)=1,6 qui est inférieure à l'écart-type de 1,9 alors que la plage supérieure (13-10,6)=2,4 est supérieure à l'écart-type.

Si nous avions pris un intervalle correspondant à 1 σ, les valeurs auraient été comprises entre 8,7 et 12,5 et les calculs auraient donné:

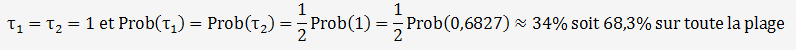
Pour 2 écarts-types, Prob(2)=0,9545, on retrouve bien 95,45% (sachant que 95% correspond à 1,96) mais l'intervalle correspondant est très supérieur aux valeurs (6,87 à 14,32 grammes et surtout en partie basse due à l'asymétrie de la la répartition).

Série 2: la moyenne est de µ = 11 grammes et la répartition est symétrique, les valeurs obtenues se trouvent sur la plage (9 à 13 grammes).

Calculons la probabilité d'obtenir des valeurs comprisent entre 9 et 11 grammes:

La probabilité Prob(9<Xi<11) est égale à ½Prob(-1,05)=½Prob(0,7063)≈35,3%

Calculons la probabilité d'obtenir des valeurs comprisent entre 11 et 13 grammes:

La probabilité Prob(11<Xi<13) est égale à Prob(9<Xi<11) ≈35,3%

Les probabilités sont strictement identiques.

Si nous avions pris un intervalle correspondant à 1 σ, les valeurs auraient été comprises entre 9,1 et 12,9 et nous aurions le même résultat que pour la série 1: Prob(série2)≈68,3 %.

Pour l'ensemble de la plage (Xi≤ 13), la probabilité est égale à ½+½Prob(1,05)=½+½(70,63%)≈85,3%

Série 2: la moyenne est de µ = 11 grammes et la répartition est symétrique, les valeurs obtenues se trouvent sur la plage (9 à 13 grammes).

Calculons la probabilité d'obtenir des valeurs Prob(13<Xi<14 grammes), aucune valeur n'a été mesurée sur cette plage:

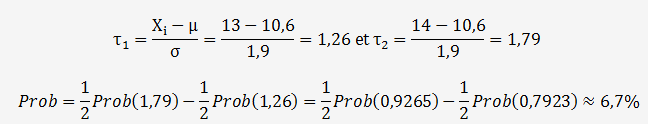
Il subsiste tout de même une probabilité de 6,7 % d'obtenir des résultats dans cette plage.

Valeurs de la probabilité en fonction de la variable aléatoire