Exemple d'estimation d'une incertitude selon ISO 98-3

Le but de l’exercice est d'estimer l'incertitude d'étalonnage d'une résistance de 1 Ω.

Méthode des 5 M:

Données :

Une résistance est étalonnée en utilisant une autre résistance de référence, les deux résistances sont connectées en série à une source de courant continu et chaque résistance reçoit la même tension.

Un voltmètre digital est utilisé pour mesurer le voltage qui traverse les deux résistances: résolution = 0,1.10-6 Volt

A l'aide d'un by-pass, chaque résistance est contrôlée l'une après l'autre.

La valeur de la résistance soumise à étalonnage sera notée RX et celle de la résistance étalon RS.

Les voltages respectifs seront notés VX et VR.

La valeur de la résistance étalon et son incertitude (k=2) sont obtenues à partir du certificat: RS=1,000004 ±2,5.10-6 ohms à 20°C.

L'incertitude sur la stabilité est de 5.10-6 ohms

Chaque mesure de voltage sera mesurée 10 fois pour chaque résistance.

Préambule:

Etant donné que la même tension circule dans les résistances, on peut écrire:

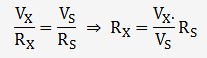
Les facteurs contribuant à l'incertitude de mesure sont:

- L'incertitude sur les mesures répétées de VX

- L'incertitude sur les mesures répétées de VS

- L'incertitude liée à la résolution de lecture du Voltmètre

- Précision constructeur du voltmètre (0,025% +2 digits) de la valeur lue, on considérera que les 2 digits intégrent la résolution de lecture

- L'incertitude liée à la valeur certifiée de la résistance de référence

- L'incertitude liée à la stabilité de la valeur de référence

- L'incertitude liée à la différence de température entre le laboratoire et la température utilisée lors de l'étalonnage de la résistance de référence

L'incertitude sur RX s'exprime avec la relation:

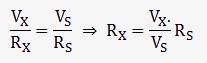
Résultat des mesurages:

N°	VX (mV)	VS (mV)
1	99,91963	99,92478
2	99,91970	99,92474
3	99,91968	99,92470
4	99,91977	99,92492
5	99,91986	99,92488
6	99,92058	99,92561
7	99,92055	99,92558
8	99,92008	99,92506
9	99,91987	99,92479
10	99,91968	99,92468
Moyenne	99,919940	99,924974
Ecart-type	3,544.10-4	3,461.10-4

 

Les incertitudes de type A en mV liées à la répétabilité sont données par les relations:

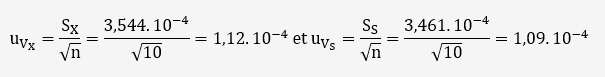
Le degré de liberté est de 9:(n-1=10-1)

Calcul de la résistance RX:

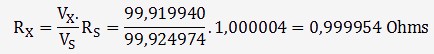
Détermination de l'incertitude sur RX:

Nous allons dériver la fonction de RX, ce qui donne les coefficients de sensibilité suivants:

L'incertitude liée à la précision du voltmètre est comptée 2 fois (pour chaque résistance) et suit une distribution rectangulaire et vaut pour une tension d'environ 100 mV:

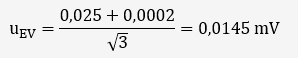
L'incertitude de la résistance de référence suit une loi normale et doit donc être divisée par deux pour être utilisée:

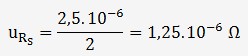
L'incertitude sur la stabilité suit une distribution rectangulaire et vaut:

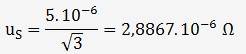
L'incertitude liée à la température sera considérée comme négligeable car l'étalonnage a été réalisée dans les conditions du certificat de la résistance de référence: 20°C.

En reprenant la somme quadratique des différentes composantes, on obtient:

Avec un facteur d'élargissement k = 2, URX = 4.10-4 Ω.

Nous n'avons fait que 10 essais, il faut donc vérifier si nous pouvons prendre un facteur d'élargissement K = 2 avec la formule de Welch-Sattertwaite:

Le degré de liberté est suffisamment grand, la valeur de la résistance peut donc s'écrire: RX = (0,9999± 0,0004) Ω

Effet de corrélation lors des mesures de VX et VS:

En effet, nous avons utilisé le même voltmètre lors des mesurages et les mesures ont été réalisées en même temps, les variables VX et VS sont donc corrélées.

Nous devons donc déterminer le coefficient de corrélation (voir Exemple de propagation des erreurs) des données pour appliquer la loi de propagation de l'incertitude (2eme ordre de la série de Taylor).

Il nous faut calculer les différences suivantes:

N°
1	99,91963 - 99,919940	99,92478 - 99,924974	6,014.10-8
2	99,91970 - 99,919940	99,92474 - 99,924974	5,616.10-8
3	99,91968 - 99,919940	99,92470 - 99,924974	7,124.10-8
4	99,91977 - 99,919940	99,92492 - 99,924974	9,18.10-8
5	99,91986 - 99,919940	99,92488 - 99,924974	7,52.10-8
6	99,92058 - 99,919940	99,92561 - 99,924974	40,704.10-8
7	99,92055 - 99,919940	99,92558 - 99,924974	36,966.10-8
8	99,92008 - 99,919940	99,92506 - 99,924974	1,204.10-8
9	99,91987 - 99,919940	99,92479 - 99,924974	1,288.10-8
10	99,91968 - 99,919940	99,92468 - 99,924974	7,644.10-8
Somme	/	/	108,23.10-8
n(n-1)	/	/	90
Somme /n(n-1)	/	/	1,202.10-8

 

Calculons le coefficient de corrélation:

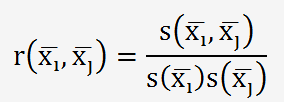
r = 0,109 (le coefficient est plus proche de 0 que de 1, les données ne sont pas très corrélées).

Si l'on poursuit l'estimation du terme du second ordre, cela donne:

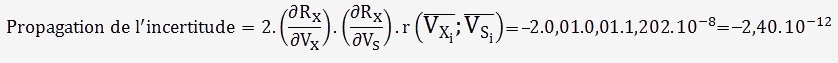
Quantité negligeable qu'il faut rajouter à l'incertitude initialement estimée:

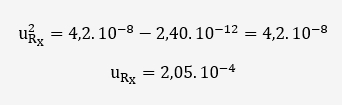
Avec un facteur d'élargissement k = 2, URX = 4.10-4 Ω.

La valeur de la résistance peut donc s'écrire: RX = (0,9999± 0,0004) Ω.