Les études R&R: Méthode ANOVA
La méthode ANOVA (ANalysis Of VAriance), est préférée à la méthode des étendues et des moyennes. Elle quantifie l'interaction entre la répétabilité et la reproductibilité et est considérée comme plus précise que la méthode des étendues et des moyennes.
Pour quantifier la répétabilité et de la reproductibilité en utilisant la méthode ANOVA, plusieurs pièces, un moyen de mesure, des opérateurs et des mesurages sont nécessaires.
La méthode recommandée est d'utiliser 10 pièces, 3 opérateurs et 3 séries de mesure, pour un total de 90 mesures.
La méthode ANOVA utilise les techniques statistiques (Test de Fisher) pour analyser les effets des différents facteurs dans les mesurages.
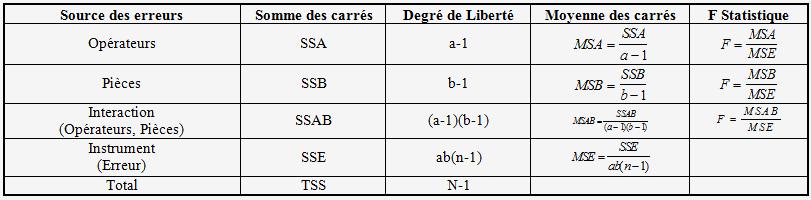
a = nombre d’opérateurs = 3,
b = nombre de pièces = 10,
n = nombre d’essais = 3,
N = nombre totale d’essai (abn) = 90.
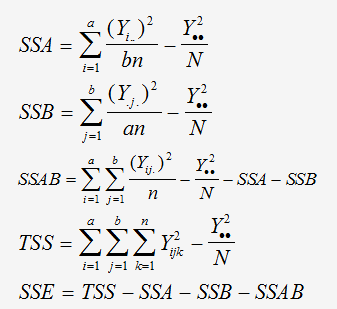
La répétabilité EV du système de mesure est donnée par la formule:
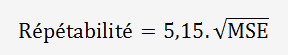
La reproductibilité AV du système de mesure est donnée par la formule:
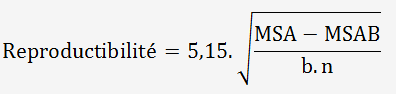
L’interaction entre les opérateurs et les pièces est donnée par :
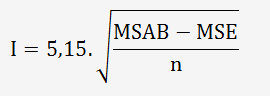
La répétabilité et la reproductibilité sont données par la formule:
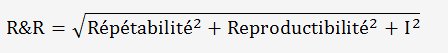
La variabilité liée à la pièce est donnée par la formule:
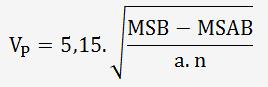
La variabilité totale est donnée par la combinaison quadratique de la variabilité du système de mesure et de la pièce:
![]()
![]()
3 opérateurs OP1, OP2 et OP3 mesurent une côte L de 45 mm avec un pied à coulisse raccordé, la tolérance de la côte est de ± 1 mm.
| N° de la mesure |
OP1 |
x̄
|
R1 |
OP2 |
x̄ |
R2 |
OP3 |
x̄ |
R3 |
|
R̄ |
||||||
| 1 |
45,08 |
45,10 |
45,09 |
45,09 |
0,02 |
45,01 |
45,04 |
45,02 |
45,02 |
0,03 |
45,04 |
45,07 |
45,07 |
45,06 |
0,03 |
45,06 |
0,027 |
| 2 |
44,94 |
44,97 |
44,93 |
44,95 |
0,04 |
44,92 |
44,95 |
44,95 |
44,94 |
0,03 |
44,92 |
44,97 |
44,91 |
44,93 |
0,06 |
44,94 |
0,043 |
| 3 |
45,08 |
45,11 |
45,13 |
45,11 |
0,05 |
44,95 |
45,11 |
45,11 |
45,06 |
0,16 |
45,10 |
45,12 |
45,11 |
45,11 |
0,02 |
45,09 |
0,077 |
| 4 |
44,97 |
45,02 |
45,01 |
45,00 |
0,05 |
45,01 |
44,93 |
45,00 |
44,98 |
0,08 |
45,02 |
44,99 |
44,99 |
45,00 |
0,03 |
44,99 |
0,053 |
| 5 |
44,92 |
44,95 |
45,01 |
44,96 |
0,09 |
44,95 |
44,99 |
44,97 |
44,97 |
0,04 |
44,99 |
44,97 |
44,95 |
44,97 |
0,04 |
44,97 |
0,057 |
| 6 |
45,03 |
45,06 |
45,05 |
45,05 |
0,03 |
45,04 |
45,06 |
44,99 |
45,03 |
0,07 |
45,07 |
45,03 |
45,02 |
45,04 |
0,05 |
45,04 |
0,050 |
| 7 |
45,24 |
45,36 |
45,31 |
45,30 |
0,12 |
45,12 |
45,21 |
45,32 |
45,22 |
0,20 |
45,26 |
45,29 |
45,28 |
45,28 |
0,03 |
45,27 |
0,117 |
| 8 |
45,16 |
45,16 |
45,10 |
45,14 |
0,06 |
45,12 |
45,13 |
45,13 |
45,13 |
0,01 |
45,13 |
45,13 |
45,14 |
45,13 |
0,01 |
45,13 |
0,027 |
| 9 |
45,20 |
45,20 |
45,24 |
45,21 |
0,04 |
45,06 |
45,19 |
45,24 |
45,16 |
0,18 |
45,19 |
45,17 |
45,16 |
45,17 |
0,03 |
45,18 |
0,083 |
| 10 |
45,07 |
45,10 |
45,05 |
45,07 |
0,05 |
45,02 |
45,05 |
45,09 |
45,05 |
0,07 |
45,10 |
45,10 |
45,09 |
45,10 |
0,01 |
45,07 |
0,043 |
| 45,09 |
0,055 |
|
45,06 |
0,087 |
45,08 |
0,031 |
|||||||||||
|
|
R̄1 |
|
R̄2 |
|
R̄3 |
||||||||||||
|
Moyenne générale |
|
45,07 |
|
0,058
|
|||||||||||||
Calcul de SSA:
La somme de toutes les valeurs de OP1 est de : 1352,64
La somme de toutes les valeurs de OP2 est de : 1351,68
La somme de toutes les valeurs de OP3 est de : 1352,38
La somme de toutes les valeurs des 3 opérateurs est de : 4056,7
b = 10 , n = 3 et N = 90
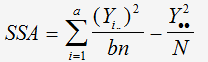
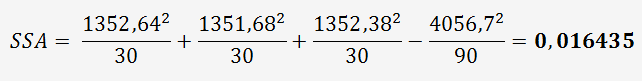
Calcul de SSB:
La somme au carré moyenne des 9 mesures (3 OP) pour
la pièce N°1 est de :
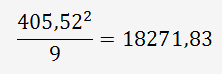
La somme au carré moyenne des 9 mesures (3 OP) pour la pièce N°2 est de :
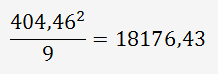
------------------
N°3 : 18298,87 ; N°4 : 18219,60 ; N°5 : 18198,01 ; N°6 : 18256,51
; N°7 : 18440,73 ; N°8 : 18333,16 ; N°9 : 18373,80
------------------
La somme au carré moyenne des 9 mesures (3 OP) pour la pièce N°10 est de :
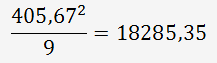
La somme totale pour les 10 pièces est de :
18271,83 + 18176,43 + 18298,87 + 18219,60 + 18198,01 + 18256,51
+ 18440,73 + 18333,16 + 18373,80 + 18285,35 = 182854,3082
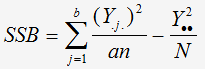
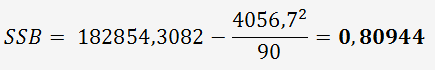
Calcul de SSAB :
La somme au carré moyenne des 3 essais pour chaque opérateur et pour chaque pièce est de :
Pièce N°1/OP1 : (45,08 + 45,10 + 45,09)²/3
= 6099,32
Pièce N°2/OP1 : (44,94 + 44,97 + 44,93)²/3 = 6060,61
Pièce N°3/OP1 : 6103,83
Pièce N°4/OP1 : 6075,00
Pièce N°5/OP1 : 6064,20
Pièce N°6/OP1 : 6087,61
Pièce N°7/OP1 : 6151,18
Pièce N°8/OP1 : 6112,86
Pièce N°9/OP1 : 6132,74
Pièce N°10/OP1 : 6094,82
Pièce N°1/OP2 : 6081,30
Pièce N°2/OP2 : 6058,81
Pièce N°3/OP2 : 6090,31
Pièce N°4/OP2 : 6069,30
Pièce N°5/OP2 : 6066,90
Pièce N°6/OP2 : 6083,10
Pièce N°7/OP2 : 6133,64
Pièce N°8/OP2 : 6109,25
Pièce N°9/OP2 : 6119,18
Pièce N°10/OP2 : 6089,40
Pièce N°1/OP3 : 6091,21
Pièce N°2/OP3 : 6057,01
Pièce N°3/OP3 : 6104,74
Pièce N°4/OP3 : 6075,00
Pièce N°5/OP3 : 6066,90
Pièce N°6/OP3 : 6085,80
Pièce N°7/OP3 : 6149,93
Pièce N°8/OP3 : 6111,05
Pièce N°9/OP3 : 6121,89
Pièce N°10/OP3 : 6101,13
La somme totale est de : 182854,3411
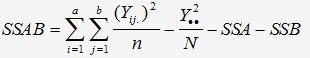
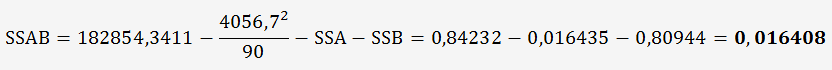
Calcul de TSS:
La somme au carré de toutes les valeurs obtenues par les 3 opérateurs = 182854,4334
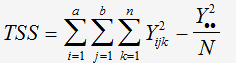
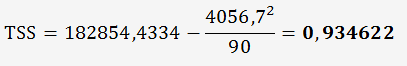
Calcul de SSE:
![]()
SSE = 0,934622 - 0,016435 - 0,80944 - 0,016408 = 0,09234
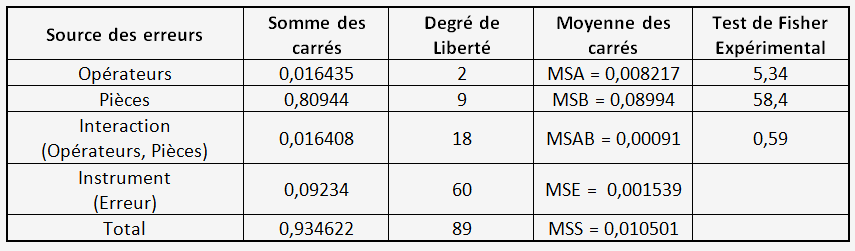
Le test de Fisher doit être inférieur à la valeur critique fournie dans la Table de Fisher-Snedecor pour un risque α = 0,05.
Cette loi ou son inverse est directement fournie par Excel® et s’appuie sur les degrés de liberté des variances:
par exemple pour F=MSA/MSE, Test de Fisher = INVERSE.LOI.F(0,05;2;60) = 3,12 < 5,34
Significatif : OUI (on ne peut pas accepter l’hypothèse nulle)
F=MSB/MSE, Test de Fisher = INVERSE.LOI.F(0,05;9;60) = 2,04 < 58,4
Significatif : OUI (on ne peut pas accepter l’hypothèse nulle)
F=MSAB/MSE Test de Fisher = INVERSE.LOI.F(0,05;18;60) = 1,78 > 0,59
Significatif : NON (on peut accepter l’hypothèse
nulle)
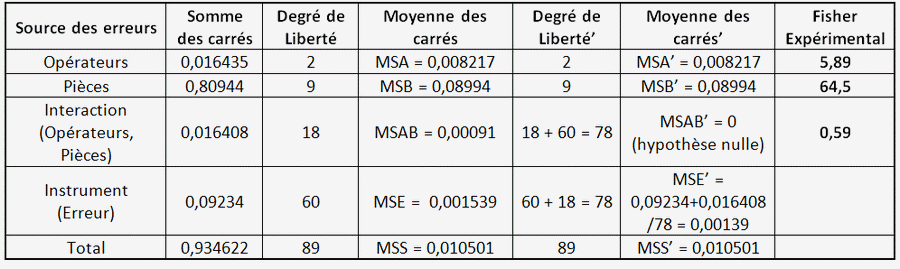
F=MSA'/MSE', Test de Ficher = INVERSE.LOI.F(0,05;2;78) = 3,11 < 5,89
Significatif : OUI (on ne peut pas accepter l’hypothèse
nulle)
F=MSB'/MSE', Test de Ficher = INVERSE.LOI.F(0,05;9;78) = 2,00 < 64,5
Significatif : OUI (on ne peut pas accepter l’hypothèse
nulle)
F=MSAB/MSE, Test de Fisher = INVERSE.LOI.F(0,05;18;60) = 1,78 > 0,59
Significatif : NON (on peut accepter l’hypothèse nulle)
Calcul des risques:
Fisher Expérimental = 64,5 et degré de liberté de SSB
= 9 et degré de liberté de SSE' = 78
Pour les pièces: Risque = LOI.F(64,5;9;78) = 0
Fisher Expérimental = 5,89 et degré de liberté de SSA = 2 et degré de liberté de SSE' = 78
Pour les opérateurs; Risque = LOI.F(5,89;2;78) = 0,004
Fisher Expérimental = 0,59 et degré de liberté de SSAB = 18 et degré de liberté de MSE = 60
Interaction Pièces/Opérateurs: Risque = LOI.F(0,59;18;60) = 0,891
Effets significatifs:
Pièces = OUI car 64,5 > 2
Opérateurs = OUI car 5,89 > 3,11
Interaction Pièces/Opérateurs = NON car 0,59 < 1,78
Calculons la répétabilité du système de mesure (EV):
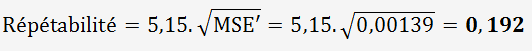
Calculons la reproductibilité du système de mesure (AV):

Calculons l’interaction entre les opérateurs et les pièces:
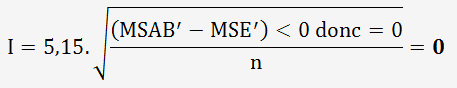
Calculons le R&R:

Calculons la variabilité liée à la pièce:
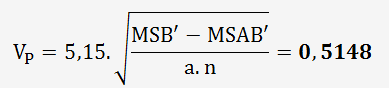
Calculons la variabilité totale:
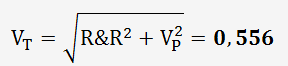
![]()
Nous en déduisons les % des contributions :
%EV= (EV/VT).100 = (0,192/0,556).100 = 34,5% (Equipement)
%AV=(AV/VT).100 = (0,0852/0,556).100 = 15,3% (Opérateur)
%R&R = (R&R/VT).100 = (0,21/0,556).100 = 37,8%
%Interaction=(0/0,556).100 = 0 % (Pièce/Opérateur)
%VP = (VP/VT).100 = (0,5148/0,556).100 = 92,6% (Produit)
Si le pourcentage R&R est:
< 10 %: le processus est satisfaisant
Compris entre 10 et 30%: le processus est acceptable mais on peut l'améliorer
> 30%: le processus est inacceptable (ce qui est le cas)
Dans le cas présent, le processus est dégradé par la répétabilité des opérateurs qui n'est pas optimale, cela peut s'expliquer par un instrument mal adapté au type de cote ou une prise de cote qui ne permet pas d'être répétable (zone de forme complexe, positionnement imprécis de l'instrument).
Si l’analyse porte sur le Produit, la Tolérance
est utilisée en lieu et place de la Variation Totale.
Les deux approches VT et Tolérance sont valables, elles
dépendent de l’utilisation du système de mesure et du
souhait du client.
Dans le cas d’une analyse basée sur la VT, il faut s’assurer que les pièces mesurées représentent bien la Variation Totale du Procédé.
Tolérance = IT = 2
%TOL EV = (0,192/2).100 = 9,6%
%TOL AV = (0,0852/2).100 = 4,3%
%R&R = (0,21/2).100 = 10,5%
%Interaction=(0/2).100 = 0 %
%VP = (0,5148/2).100 = 25,7%
Dans le cas présent, l'analyse sur le produit est acceptable.
