Les intervalles des vérifications

Les intervalles de vérification ou d'étalonnage font souvent couler beaucoup d'encre, doit-on systématiquement faire vérifier son matériel chaque année?

Il n'existe malheureusement que deux alternatives à cette question:

- la première est souvent imposée par la norme d'essai et/ou la méthode d'étalonnage du matériel qui stipule par exemple que l'intervalle d'étalonnage ne devra pas excéder 12 mois (pour un évaluateur, la dérive ne devra pas être trop importante, car il pourrait considérer que l'équipement n'est pas sous contrôle, à moins d'argumenter ce dépassement par une dérogation par exemple).

A noter que certains laboratoires ont demandés à l'organisme notifié de pourvoir espacer le raccordement de certains équipements car le nombre d'essais ne permettait pas de payer la prestation de raccordement annuel, l'intervalle a donc été rallongé et ces équipements sont donc raccordés tous les deux ans. L'éventuelle dérive va t'elle pénaliser les résultats des essais, je ne pense pas, à condition bien sûr de mettre en place des vérifications périodiques pour maîtriser la réponse de l'équipement.

- la seconde plus libre consiste à choisir un intervalle de raccordement approprié pour chaque équipement si les normes n'imposent rien, c'est sur le choix de cet intervalle que nous allons le développer le contenu ci-dessous.

En règle générale, l'intervalle de raccordement repose sur plusieurs critères:

- L'exigence du client pour des mesures précises, fiable et de qualité.

- La dérive de l'équipement sur les années précédentes.

- Les habitudes de la profession sur des équipements similaires.

- L'obligation de réduire les coûts d'étalonnage, une exigence émanant généralement de la direction vis-à-vis des coûts externes qui augmentent et tirent la marge vers le bas.

Satisfaire à tous les critères est souvent difficile, il faut ajuster des intervalles d'étalonnage qui favorisent à la fois la qualité des prestations et les objectifs de réduction des coûts.

Concept de base

Le lecteur peut également consulter le document:"Optimisation des périodicités d’étalonnage: La méthode Opperet" auprès du CFM.

Le concept de ce document ne repose pas sur cette méthode.

La mesure avec laquelle la valeur d'un paramètre donné peut être connue lors de l'étalonnage est déterminée par un certain nombre de variables. Il s'agit notamment de l'incertitude de l'étalonnage de l'équipement, de la précision avec laquelle les mesures peuvent être réalisées, la stabilité du processus de mesure, l'habileté de la personne effectuant l'étalonnage, etc...
Immédiatement après étalonnage, la connaissance de la valeur de ce paramètre est liée à une série de valeurs (fonction) qui peuvent être assez bien définies.
Après un certain temps, cette fonction est moins précise. En raison des processus aléatoires inhérents aux essais et à la diversité des mesures et de l'environnement de l'équipement, les valeurs du paramètre ont tendance à varier de façon aléatoire.
Cette variation aléatoire propage la distribution des valeurs d'origines du paramètre et au fil du temps, la propagation des valeurs augmente.

Ainsi, l'incertitude entourant la valeur du paramètre étalonné grandit à mesure que le temps s'écoule depuis le dernier étalonnage.

Les laboratoires concernés principalement par l'intégrité de la mesure ont tendance à mettre des intervalles entre étalonnages souvent plus courts, ce qui n'est pas forcément justifiable économiquement.
Inversement, dans les laboratoires qui se préoccupent principalement de l'aspect économique plutôt que de l'intégrité de la mesure, les intervalles entre les étalonnages ont souvent tendance à être plus long, ce qui peut s'avérer préjudiciable vis-à-vis de l'incertitude de la mesure.

Système d'analyse de l'intervalle d'étalonnage

L'objectif de tout système d'analyse de l'intervalle d'étalonnage devrait être que le coût à chaque intervalle est maintenu à un minimum.

Cette exigence, lorsqu'elle est couplée avec celle d'atteindre les objectifs de fiabilité de la mesure, conduit aux objectifs suivants:

- Mise en place d'objectifs appropriés à la fiabilité des mesures
- Ajustement des intervalles permettant d'atteindre les objectifs de fiabilité
- Emploi d'algorithmes et de méthodes qui permettent d'obtenir des intervalles appropriés dans les plus brefs délais
- Intervalles d'étalonnage déterminés avec un minimum d'intervention humaine.

La mise en place d'une telle stratégie requiert les éléments suivants:

• Collecte et stockage des données (déduction de la dépendance temporelle sur l'augmentation de l'incertitude de mesure).

• Modélisation de la fiabilité (utilisation d'un modèle statistique pour faciliter la détermination des intervalles d'étalonnage).

• L'analyse statistique des résultats d'étalonnage (Les méthodes statistiques sont utilisées pour ajuster les modèles de fiabilité des données et d'identifier les circonstances aberrantes ou exceptionnelles).

• Coût / avantages (Ces méthodes permettent d'optimiser la fréquence d'étalonnage et par conséquent les coûts externes).

• Les besoins en personnel (une connaissance en statistique est préférable pour le personnel qui déterminera l'intervalle d'étalonnage).

• La formation et la communication (une bonne compréhension des principes de l'augmentation de l'incertitude et une appréciation de la façon dont les données d'étalonnage sont utilisées pour établir et ajuster les intervalles sont nécessaires pour favoriser l'exactitude des données).

Modélisation de la fiabilité d'un équipement:

L'amplification de l'incertitude de mesure d'un paramètre à l'instant t est inscrit dans sa fonction de densité de probabilité statistique f(x(t)).

En considérant la représentation de la fiabilité de la mesure: R (t) à l'instant t et les limites de tolérance L1 et L2 du paramètre, la relation entre la fiabilité de la mesure et f(x(t)) est donnée par l'intégrale:

La fiabilité de la mesure est la probabilité qu'un paramètre fonctionne dans un état hors-tolérance.

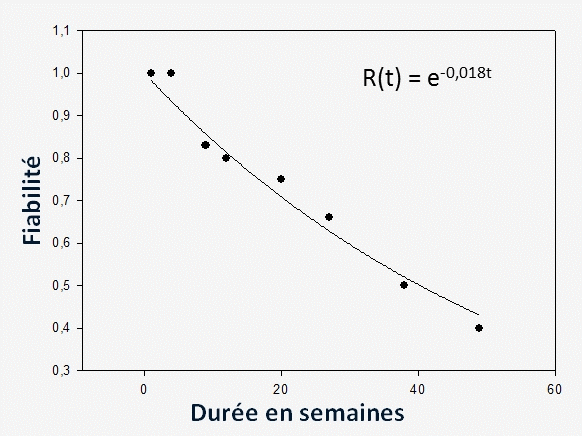
À un moment t donné et écoulé depuis l'étalonnage, la probabilité peut être échantillonnée en effectuant un certain nombre d'étalonnages n(t). Si le nombre d'étalonnages pour lequel le paramètre a été trouvé dans la tolérance est représenté par g(t), alors la fiabilité de la mesure à l'instant t est:

Avec une loi exponentielle, la probabilité d'un instrument de ne pas être hors tolérance pendant un intervalle de temps ti est donnée par:

(1) R(pas de problème avant t)=R0exp-λt avec λ= Taux de défaillance.

Prenons un exemple chiffré pour expliquer la démarche et partons du principe qu'à t=1 semaine, g(t)/n(t)=R0=1.

N° de semaines dans l'année (t)	Nombre d'étalonnages effectués n(t)	Nombre d'étalonnages dans les tolérances g(t)	Fiabilité mesurée R(t)
1	1	1	1,00
4	6	6	1,00
9	5	5	1,00
12	4	4	1,00
20	4	3	0,75
27	6	4	0,66
38	6	3	0,50
49	5	2	0,40

 

Approche simple:

Commençons avec des calculs pouvant être appliqués sans connaissance particulière:

Nous allons déterminer le taux de défaillance de notre équipement donc λ en calculant le nombre total d'étalonnage N et le nombre total d'étalonnage G dans les tolérances.

Faisons les calculs:N=∑n=(1+6+5+4+4+6+6+5)=37 et G=∑g=(1+6+5+4+3+4+3+2)=28.

Ensuite, nous allons calculés la moyenne du temps T des étalonnages, il s'agit d'une moyenne pondérée qui se calcule avec la formule:

T=1/Nx∑tjnj=1/37x(1x1+4x6+9x5+12x4+20x4+27x6+38x6+49x5)=1/37x833=22,5 semaines

La proportion d'étalonnage hors tolérance pendant le temps T peut se calculer approximativement par la formule:

R(pas de problème avant T)≈G/N≈28/37≈0,75

En utilisant l'équation exponentielle (1), on peut écrire: G/N=exp-λoT avec λ0 l'estimation de λ

On peut donc en déduire: λ0=-1/TxLn(G/N)=-1/22,5xLn(0,72)=0,0124

Par conséquent: R(t)=exp-0,0124t

Approche plus scientifique:

Plusieurs modèles sont utilisés pour représenter l'évolution de l'incertitude dans le temps: exponentielle, Weibull,..

R(t)=Roexp-λt est la modélisation exponentielle qui se caractérise par Ro et λ: R0 est la fiabilité à t=0 et λ est le taux de défaillance.

Elle s'utilise lorsque le taux d'étalonnage hors tolérance est constant avec le temps (voir les différentes modélisations en bas de page)

Nous devons modéliser la fonction R(t)=f(t) avec EXCEL, on peut voir avec une loi exponentielle de type R(t)=Roexp-λt que λ0=0,017 (l'estimation plus simpliste n'est pas mauvaise: écart de 0,0017).

Il faut dans les conditions forcer EXCEL à passer par 1 pour que R0 soit égal à 1.

Attention, pour certaines modélisations, EXCEL sera limité pour plusieurs raisons: la formule plus compliquée n'existera pas dans les propositions, EXCEL ne réitère pas la modélidation pour une estimation plus juste, les conditions limites ne peuvent pas toujours être imposées et dans ce cas, il faudra utilisé un logiciel plus puissant tel que SIGMAPLOT par exemple.

Mais que fait-on avec cette équation?

Calcul des limites de confiances avec une probabilité de 95%

Je ne vais pas développer la démonstration mathématique de la formule utilisée pour estimer la probabilité maximale à partir de la probabilité qu'un instrument soit encore conforme après une durée t d'utilisation.

Je vous donne seulement la formule de base qui repose sur une loi de probabilité binomiale:

avec

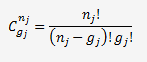
La probabilité maximale s'obtient en dérivant la probabilité de R et en utilisant une estimation de λ à partir de λ0.

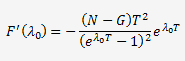
L'erreur sur λ0 est obtenue par la dérivée seconde de F'(λo)

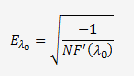
La limite basse et haute de λo est donnée par:

K est le facteur d'élargissement qui sera pris égale à 1,96 pour un niveau de confiance de 95%.

Passons à quelques applications numériques et calculons F'(λ0):

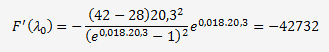
Eλo =0,000746

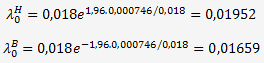
Nous avons vu que la fiabilité d'un équipement était donné par R(t)=exp-λt

On peut en déduire que:

Et que par conséquent:

L'erreur sur t0 peut être estimé par:

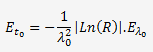
La limite basse et haute de t0 est donnée par:

Passons à quelques applications numériques et calculons to pour une fiabilité R=0,85:

Nous savons que: λ0=0,018; Eλ0 =0,000746 donc:

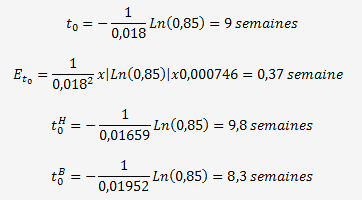
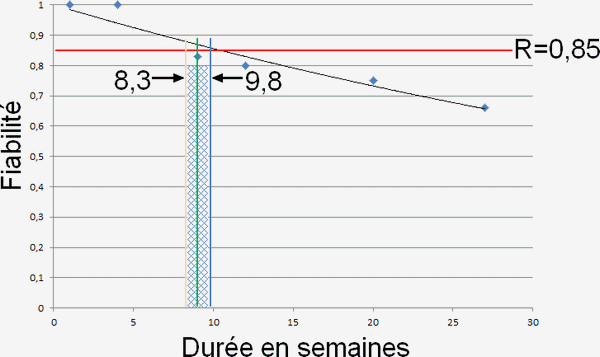
Pour une fiabilité de R=0.85, l'intervalle de vérification ou d'étalonnage avec une probabilité de 95% est de 9 semaines avec une tolérance générale de 1,5 semaine.

On peut bien sûr effectuer les mêmes calculs avec λ mais il faudra utiliser un programme pour déterminer la probabilité de L selon:

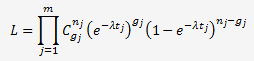
Les résultats seront légèrement différents mais l'estimation avec λ0 est suffisamment précise.

Modèle de Weilbull

avec β = facteur de forme