Validation d'un processus de mesurage
La technologie évolue, votre équipement est en fin de vie, la direction souhaite étendre le domaine de vos activités à d'autres grandeurs physiques ou paramètres, une exigence réglementaire se transforme en opportunité de chiffre d'affaires, bref, un nouvel équipement arrive dans le laboratoire dans quelques jours.
Il va falloir mettre en œuvre un processus de validation pour répondre à certains paragraphes de la norme: §6.4.5, 7.2.1.5 et 7.2.2.3.
Nous allons détailler les différentes étapes pour obtenir l'assurance de vérifier l'ensemble des points critiques du processus de mesurage.
Cette validation se traduit pas 6 étapes distinctes:
1) la spécificité ou la sélectivité:
Il s'agit de la capacité d'une méthode analytique de différencier et de quantifier l'analyte en présence d'autres composants/éléments dans la matrice.
Il faut connaître la contribution des interférents qui peuvent se traduire pas des résultats erronés (mesure faussée par la présence d'un autre élément chimique, ou mesure d'un autre élement chimique), cette contribution ne doit généralement pas dépasser 3 % de la réponse de l'élément recherché et être inférieure à la limite de quantification (LDQ).
En fonction des procédés analytiques, ces interférences peuvent être majorantes ou minorantes et lorsque cela est possible, pour mesurer son impact, on peut citer:
- Une technique par ajout dosé permet généralement de vérifier si la contribution existe,
- Une analyse dans une bande spectrale différente (sous UV par exemple en réalisant l'analyse sous gaz neutre),
- Passage d'un étalon (MRC) identique (liquide, gazeux ou solide) à la matrice analysée,
- Obtenir le même résultat avec une autre technique analytique.
2) la linéarité:
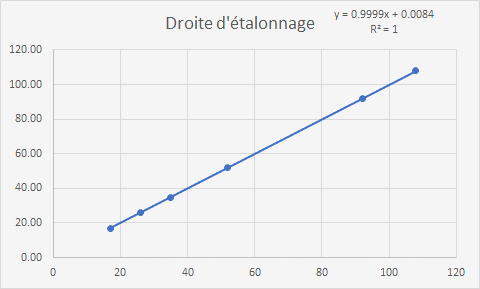
L'équation de la courbe d'étalonnage (incluant la droite) doit avoir un coefficient de corrélation R le plus proche de 1, c'est-à-dire que la différence entre la réponse instrumentale et les concentrations connues doit être la plus faible possible.
L'étalonnage réalisée sur une plage appropriée (tributaire à la fois de l'équipement, de l'élément recherché et du domaine de concentration recherché) doit pouvoir encadrer la concentration la plus basse (LIDQ) et la plus élevée, le nombre de points (généralement = 6) pour établir la relation entre la concentration et la grandeur physique propre à chaque équipement et à chaque capteur doit être suffisant pour garantir que la réponse soit continue, reproductible et sans équivoque pour chaque point d'intérêt.
On peut également insérer un "blanc" (ne contient ni l'élément recherché, ni la matrice) et un échantillon "zéro" (contient la matrice sans l'élément recherché).
Il est généralement difficile de trouver des MRC adéquates car si l'élément n'est pas analysé, cela ne signifie pas forcément qu'il n'est pas présent sous forme de trace.
On pourra utiliser un MRC qui contient une très faible concentration de l'élément recherché.
L'étalon le plus bas sur la courbe d'étalonnage doit être accepté comme LDQ si les conditions suivantes sont remplies:
- La réponse analytique de la LDQ doit être au moins cinq fois supérieure à la réponse sur le blanc.
- La LDQ ne doit pas être confondue avec la LDD (limite de détection).
3) Le taux de récupération: c'est le degré auquel la valeur mesurée pour l'analyte dans un échantillon correspond à la valeur acceptée, vraie ou de référence, il s'exprime la plupart du temps en relatif, cette donnée n'est pas impérative et est intégrée si l'on souhaite déterminer l'écart-type liée à l'erreur de la courbe d'étalonnage.
4) La répétabilité: elle est déterminée par une analyse répétée d'échantillons contenant des quantités connues de l'analyte et doit être mesurée à l'aide d'un minimum de cinq déterminations par concentration.
5) Limite de détection (LDD): c'est la plus petite concentration de l’élément recherché (analyte) pouvant être détectée, mais non nécessairement quantifiée, dans les conditions expérimentales décrites de la méthode, elle est différente du blanc.
Elle présente deux risques:
1) de considérer que l'élément analysé est présent alors que sa concentration est nulle (risque α)
2) de considérer que sa concentration est nulle alors qu'elle ne l'est pas (risque ß)
La LDD pour la plus petite concentration est donné par la formule suivante (SD représente l'écart-type de la série):
LDD = X + (3.SD)
6) Limité de quantification (LDQ): c'est la plus petite ou la plus grande concentration de l’analyte pouvant être quantifiée avec une incertitude acceptable, dans les conditions expérimentales décrites de la méthode.
Cette détermination doit être réalisée à minima entre 6 et 10 fois, la réponse moyenne X et l'écart-type SD des n résultats sont calculés.
la LDQ pour la plus petite concentration est donné par la formule suivante:
LDQ = X + (10.SD)
Prenons un exemple concret:
Le laboratoire a reçu son nouvel équipement, il est installé et fonctionnel, le personnel a été formé.
L'équipement mesure la teneur en Hydrogène dans des alliages de Titane.
Les MRC ont été achetés auprès d'un fournisseur accrédité ISO 17034: (3; 17; 26; 35; 52; 92; et 108 ppm d'hydrogène dans des alliages de titane).
La teneur de 3 ppm servira à simuler le blanc.
La résolution de l'afficheur est de 0,01 ppm.
1) la spécificité ou la sélectivité: dans le cas présent, après combustion, l'hydrogène gazeux est oxydé en H2O et la sélectivité est assurée par la cellule en proche infrarouge.
Pour réduire les interférences et la dérive de l'instrument, la cellule IR de mesure est purgée par le gaz vecteur (Hélium) avant chaque analyse.
2) la linéarité:
Le technicien a réalisé un étalonnage de l'équipement en analysant p=3 répliques les n=6 MRC (les bonnes pratiques imposent de réaliser 5 répliques par MRC mais la méthodologie reste la même).
Il a obtenu les résultats suivants:
Attention, des MRC peuvent donner un écart-type très différents par rapport aux autres, il sera alors nécessaire de segmenter la droite d'étalonnage pour obtenir une dispersion plus homogène.
Il calcule ensuite les différences (erreurs expérimentales) entre la valeur de chaque MRC et les 3 réponses instrumentales de l'équipement:
| MRC | 1 | 2 | 3 |
Moyenne | Eexp 1 |
Eexp 2 | Eexp 3 |
| 17 ppm | 17,01 | 17,01 | 17,05 | 17,0233 | -0,0133 | -0,0133 | 0,0267 |
| 26 ppm | 25,99 | 26,00 | 26,03 | 26,0067 | -0,0167 | -0,0067 | 0,0233 |
| 35 ppm | 34,98 | 35,00 | 34,99 | 34,9900 | -0,0100 | 0,0100 | 0,0000 |
| 52 ppm | 52,00 | 52,02 | 51,99 | 52,0033 | -0,0033 | 0,0167 | -0,0133 |
| 92 ppm | 91,99 | 92,00 | 91,99 | 91,9933 | -0,0033 | 0,0067 | -0,0033 |
| 108 ppm | 108,02 | 108,01 | 108,01 | 108,0133 | 0,0067 | -0,0033 | -0,0033 |
On va déterminer la somme des carrés de chaque
erreur expérimentale à l'aide de l'équation suivante
(Y
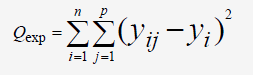
Q
L'écart-type expérimental est donné par la formule suivante:
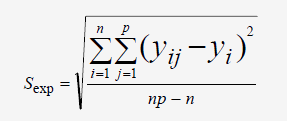
Le degré de liberté est donné par np-n ou n(p-1)=12.
S
On va déterminer la somme des carrés de l'erreur résiduelle à l'aide de l'équation suivante:
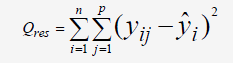
En général, une droite de type y=ax+b est utilisée et déterminée à partir de la moyenne de chacune des répliques:
| MRC | 1 | 2 | 3 |
Calculé | Eres 1 |
Eres 2 | Eres 3 |
| 17 ppm | 17,01 | 17,01 | 17,05 | 17,0067 | 0,0033 | 0,0033 | 0,0433 |
| 26 ppm | 25,99 | 26,00 | 26,03 | 26,0058 | -0,0158 | -0,0058 | 0,0242 |
| 35 ppm | 34,98 | 35,00 | 34,99 | 35,0049 | -0,0249 | -0,0049 | -0,0149 |
| 52 ppm | 52,00 | 52,02 | 51,99 | 52,0032 | -0,0032 | 0,0168 | -0,0132 |
| 92 ppm | 91,99 | 92,00 | 91,99 | 91,9992 | -0,0092 | 0,0008 | -0,0092 |
| 108 ppm | 108,02 | 108,01 | 108,01 | 107,9976 | 0,0224 | 0,0124 | 0,0124 |
Q
L'écart-type résiduel est donné par la formule suivante:
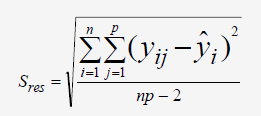
Le degré de liberté est donné par np-2 =16.
S
Détermination du défaut d'ajustement:
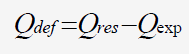
Q
L'écart-type du défaut d'alignement est estimé par la formule:
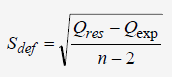
S
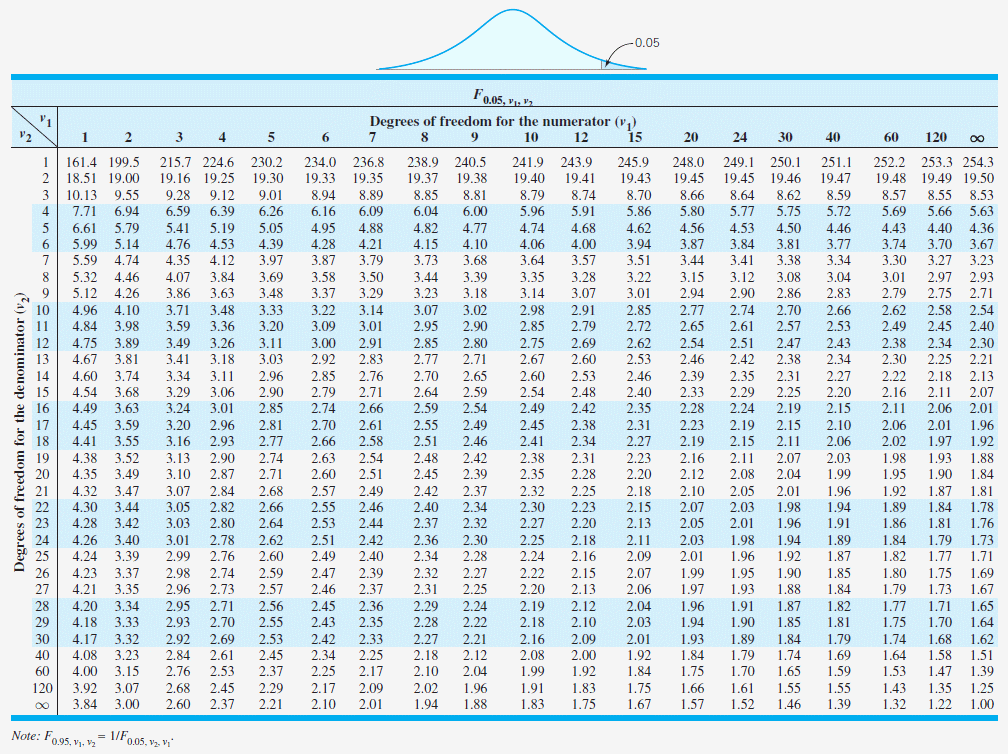
Afin de poursuivre, on va vérifier avec un test de Fischer-Snedecor que l'hypothèse de validité de la linéarité est acceptée:
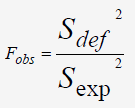
Si F
Si F
F
S
S
F
L’hypothèse de non validité du domaine de linéarité est refusée, la linéarite est donc démontrée avec une probabilité de 95%.
3) Le taux de récupération:
Détermination du coefficient de variation:
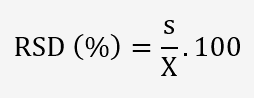
Le taux de récupération est donné par 100-RSD:
| MRC | 1 | 2 | 3 |
s | Calculé | RSD% |
TR% |
| 17 ppm | 17,01 | 17,01 | 17,05 | 0,0231 | 17,0067 | 0,136 | 99,86 |
| 26 ppm | 25,99 | 26,00 | 26,03 | 0,0208 | 26,0058 | 0,080 | 99,92 |
| 35 ppm | 34,98 | 35,00 | 34,99 | 0,0100 | 35,0049 | 0,028 | 99,97 |
| 52 ppm | 52,00 | 52,02 | 51,99 | 0,0153 | 52,0032 | 0,029 | 99,97 |
| 92 ppm | 91,99 | 92,00 | 91,99 | 0,0058 | 91,9992 | 0,0063 | 99,99 |
| 108 ppm | 108,02 | 108,01 | 108,01 | 0,0058 | 107,9976 | 0,0054 | 99,99 |
4) La répétabilité:
| MRC | 1 |
2 |
3 |
4 |
5 |
Moyenne |
Ecart-type | RSD% | TC% |
| 35 ppm | 34,98 | 35,00 | 34,99 | 35,12 | 35,05 | 35,028 | 0,058 | 0,165 | 99,83 |
Il est recommandé que le RSD soit ≤ 1% si p répliques ≥ 5.
5) Limite de détection (LDD):
Détermination de la valeur à blanc:
L'opérateur réitère 10 fois l'analyse du MRC contenant 3 ppm d'hydrogène (valeur fournie mais non certifiée)
| MRC | 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Moyenne |
Ecart-type |
| Résultats | 2,20 | 3,52 | 3,02 | 2,92 | 2,87 | 3,15 | 3,05 | 2,78 | 2,98 | 3,12 | 2,96 | 0,334 |
SD du blanc = 0,33 ppm
On peut en déduire la limite de détection: LDD = X + (3.SD) = 2,96+3.0,33 = 3,95 ppm
6) Limité de quantification (LDQ):
On peut en déduire la limite de quantification: LDD = X + (10.SD) = 2,96+10.0,33 = 6,26 ppm
Utilisation de l'équipement en routine:
Choix de 2 MRC d'une autre source que ceux utilisés pour l'étalonnage et qui encadrent les valeurs habituellement mesurés sur les échantillons inconnus:
1 - 19 ppm et 2 - 42 ppm
Résultats sur 24 jours d'utilisation sur le 42 ppm d'H2 ayant une incertitude élargie de 2,3 ppm
| N° | Résultats | N° | Résultats |
N° | Résultats | N° |
Résultats |
| 1 | 41,60 | 7 | 42,48 | 13 | 40,04 | 19 | 43,16 |
| 2 | 42,00 | 8 | 43,20 | 14 | 44,20 | 20 | 41,86 |
| 3 | 40,80 | 9 | 40,56 | 15 | 42,64 | 21 | 42,38 |
| 4 | 40,56 | 10 | 41,28 | 16 | 43,91 | 22 | 41,86 |
| 5 | 42,24 | 11 | 40,82 | 17 | 43,43 | 23 | 42,64 |
| 6 | 40,08 | 12 | 42,90 | 18 | 43,42 | 24 | 41,72 |
La moyenne des 24 résultats réalisée par 2 opérateurs de manière aléatoire est de : 42,07 ppm
L'écart-type sur les 24 résultats est de: 1,19 ppm
Biais (ou erreur de justesse) par rapport à l'étalon: 0,07 ppm
Le biais n'est pas significatif si:
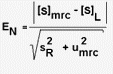 <2
<2
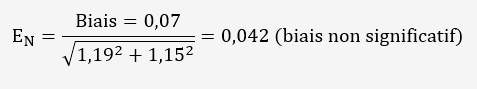
L'écart-type est considéré ici comme étant plus représentatif d'une reproductibilité (joursr différents, opérateurs différents, seul l'équipement est identique).
Détermination de l'incertitude:
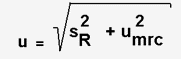
u = ±1,65 ppm soit U = ±3,31 ppm avec une probabilité de 95 % (K=2)
Détermination des limites:
Les résultats ne sont pas dispersés, on peut prendre l'écart-type comme limite de la carte de contrôle:
Limite de surveillance = 2 Ecart-types = 2,38 ppm
Limite de contrôle = 3 Ecart-types = 3,57 ppm.
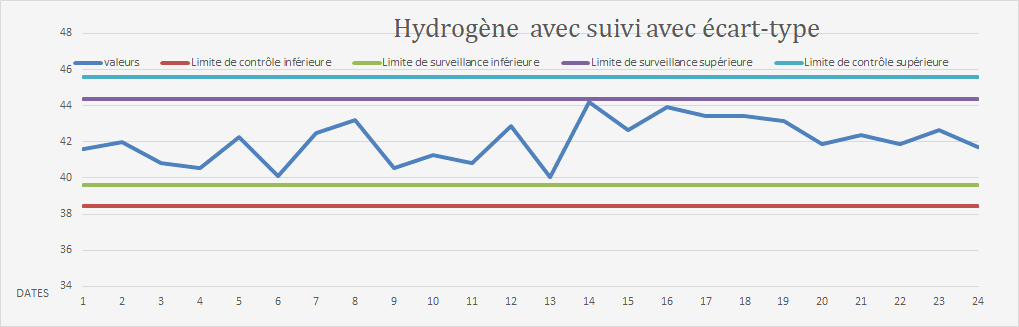
Conclusion: le processus de mesurage est sous contrôle.
Note: on peut également constater que l'incertitude est quasiment égale aux limites de contrôle, mais nous n'avons qu'un seul levier de correction (plus de valeurs pour réduire l'écart-type) car nous sommes tributaire des MRC disponibles sur le marché.
Table de Fischer-Snedecor