Surveillance périodique des équipements
La norme ISO/IEC 17025 impose une procédure pour surveiller la validité des résultats et cela se traduit généralement par des étalonnages/vérifications annuelles et autres vérifications externes (essais interlaboratoires) et internes réalisées à l'aide d'étalons pour assurer la traçabilité métrologique.
Il existe une méthode formalisée au § 7.7.1.b: utilisation d'autres instruments (comparaison inter-instruments) qui est généralement peu utilisée pour plusieurs raisons que nous allons détailler mais qui si elle est bien appliquée répond tout à fait pour assurer la traçabilité métrologique et assurer que l'équipement n'a pas dérivé, elle peut également permettre d'allonger les périodicités des vérifications externes de certains équipements.
1) la difficulté de mise en œuvre:
- Le laboratoire ne possède pas toujours deux équipements qui fournissent les mêmes résultats.
- Les grandeurs mesurées ne doivent pas être entachées d'erreurs aléatoires lors du mesurage (par exemple, comparer deux machines de traction en utilisant un matériaux de référence qui possède sa propre incertitude et dont la valeur est nettement supérieure à la classe des équipements)
- les étendues de mesure, résolution doivent être identiques, du moins sur les plages concernées.
2) le protocole:
Le plus simple est d'utiliser un étalon certifié, la traçabilité métrologique est assurée.
La méthodologie s'applique généralement à un parc machine conséquent (balances, micropipettes, ...).
Nous allons comparer la réponse de chaque équipement sur l'objet d'essai pour vérifier statistiquement que l'un d'entre eux ne dérive pas (ce qui est l'objectif de cette comparaison), un des équipement sera raccordé par un laboratoire accrédité.
Le risque existant serait que tous les équipements aient dérivé de la manière, il est donc primordial de prendre des équipements qui fonctionnent indépendamment des uns des autres.
3) Exemple avec des thermocouples:
On considère que le laboratoire possède 8 thermocouples de type J utilisés sur des équipements et au sein du laboratoire pour vérifier la température lors de la mise en œuvre de certaines méthodes d'essai.
Il dispose d'une étuve (non raccordée) dont la plage de chauffage s'étend de 25 à 250°C et d'un enregistreur numérique multivoies raccordé (résolution volontairement réduite à 0,01°C).
Il possède également un bloc d'égalisation qui permettra s'assurer que tous les thermocouples sont à la même distance dans l'étuve et qu'ils mesurent tous la même température.
La température choisie est de 50 °C, car elle représentative des températures habituellement mesurées par les thermocouples.
4) Application:
Le laborantin mesurera 5 fois la température mesurée par chaque thermocouple après 30 minutes de maintien et durant 30 minutes supplémentaires (soit une mesure toutes les 6 minutes).
Données: P=8 équipements et n = 5 mesures réalisées sur chaque thermocouples.
Le thermocouple N°2 est l'équipement de référence et son incertitude élargie est U=0,23°C pour la température de référence de 50°C.
| n\p | 1 | 2 | 3 |
4 |
5 | 6 | 7 | 8 |
| 1 | 50,01 | 50,01 | 49,95 | 50,14 | 49,99 | 50,02 | 50,03 | 50,01 |
| 2 | 50,01 | 49,99 | 50,03 | 50,12 | 50,02 | 50,01 | 50,02 | 49,99 |
| 3 | 50,00 | 49,99 | 49,99 | 50,17 | 50,04 | 50,02 | 50,00 | 50,00 |
| 4 | 49,99 | 50,00 | 49,99 | 50,08 | 50,00 | 50,03 | 50,01 | 50,02 |
| 5 | 49,99 | 49,99 | 49,99 | 50,06 | 50,02 | 50,00 | 50,02 | 50,01 |
5) Test sur les dispersions:
Nous allons utiliser le test de Mandel k:
Calcul des écarts-types pour chaque thermocouple:
| p | 1 | 2 | 3 |
4 |
5 | 6 | 7 | 8 |
| s |
0,017 | 0,009 | 0,028 | 0,044 | 0,019 | 0,011 | 0,011 | 0,011 |
Calcul de l'écart-type de répétabilité par la formule suivante:
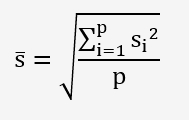
![]()
Et pour chaque équipement, nous allons déterminer la statistique de Mandel k:
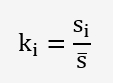
| p | 1 | 2 | 3 |
4 |
5 | 6 | 7 | 8 |
| k |
0,80 | 0,43 | 1,36 | 2,13 | 0,94 | 0,55 | 0,55 | 0,55 |
Déterminons la valeur critique de k avec la formule suivante:
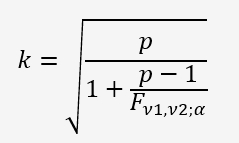
P=8, ν
Pour déterminer la valeur de Fisher qui est au dénominateur,
il faut utiliser la note sous le tableau en bas de page et par conséquent,
prendre les degrés de liberté inversés et donc: ν
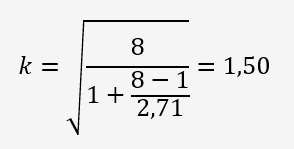
Un troisième tableau en bas de page donne directement la valeur critique de k à partir de p=5 et n=5: 1,50.
| p | 1 | 2 | 3 |
4 |
5 | 6 | 7 | 8 |
| k |
0,80 | 0,43 | 1,36 | 2,13 | 0,94 | 0,55 | 0,55 | 0,55 |
| k | 1,50 | |||||||
A ce stade, le thermocouple 4 semble pose un problème, il est écarté.
6) Second test sur les dispersions:
Calcul des écarts-types pour chaque thermocouple:
| p | 1 | 2 | 3 |
4 |
5 | 6 | 7 | 8 |
| s |
0,017 | 0,009 | 0,028 | / | 0,019 | 0,011 | 0,011 | 0,011 |
Calcul de l'écart-type de répétabilité :
![]()
Et pour chaque équipement, nous allons déterminer la statistique de Mandel k:
| p | 1 | 2 | 3 |
4 |
5 | 6 | 7 | 8 |
| k |
1,08 | 0,58 | 1,82 | / | 1,26 | 0,73 | 0,73 | 0,73 |
Déterminons la valeur critique de k :
P=7, ν
Pour déterminer la valeur de Fisher qui est au dénominateur,
il faut utiliser la note sous le tableau en bas de page et par conséquent,
prendre les degrés de liberté inversés et donc: ν
Un troisième tableau en bas de page donne directement la valeur critique de k à partir de p=7 et n=5: 1,49.
| p | 1 | 2 | 3 |
4 |
5 | 6 | 7 | 8 |
| k |
1,01 | 0,54 | 1,70 | / | 1,17 | 0,69 | 0,69 | 0,69 |
| k | 1,49 | |||||||
A ce stade, le thermocouple 3 semble poser problème, il est écarté.
7) Troisième test sur les dispersions:
Calcul des écarts-types pour chaque thermocouple:
| p | 1 | 2 | 3 |
4 |
5 | 6 | 7 | 8 |
| s |
0,017 | 0,009 | / | / | 0,019 | 0,011 | 0,011 | 0,011 |
Calcul de l'écart-type de répétabilité :
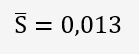
Et pour chaque équipement, nous allons déterminer la statistique de Mandel k:
| p | 1 | 2 | 3 |
4 |
5 | 6 | 7 | 8 |
| k |
1,32 | 0,70 | / | / | 1,53 | 0,90 | 0,90 | 0,90 |
Déterminons la valeur critique de k :
P=6, ν
Pour déterminer la valeur de Fisher qui est au dénominateur,
il faut utiliser la note sous le tableau en bas de page et par conséquent,
prendre les degrés de liberté inversés et donc: ν
Un troisième tableau en bas de page donne directement la valeur critique de k à partir de p=6 et n=5: 1,66.
| p | 1 | 2 | 3 |
4 |
5 | 6 | 7 | 8 |
| k |
1,32 | 0,70 | / | / | 1,53 | 0,90 | 0,90 | 0,90 |
| k | 1,66 | |||||||
A ce stade, aucun thermocouple ne pose problème.
8) Test sur les moyennes:
Nous allons utiliser le test de Mandel h:
Calcul des moyennes pour chaque thermocouple, les thermocouples N°3 et N°4 sont écartés pour ce test:
| p | 1 | 2 | 3 |
4 |
5 | 6 | 7 | 8 |
| x |
50,00 | 50,00 | / | / | 50,01 | 50,02 | 50,02 | 50,01 |
Calcul de la moyenne des moyennes:
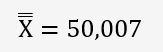
Calcul de l'écart-type des moyennes:
![]()
Pour chaque thermocouple, nous allons calculer la valeur de h avec la formule suivante:
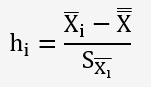
| p | 1 | 2 | 3 |
4 |
5 | 6 | 7 | 8 |
| h |
-1,19 | -1,19 | / | / | 0,70 | 0,91 | 0,91 | -0,14 |
Déterminons la valeur critique de h avec la formule suivante:
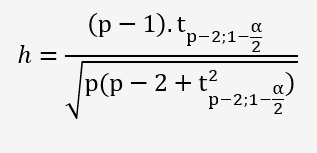
Pour un degré de liberté: p-2=6-2=4 et 0,025 (α/2), la table de Student donne une valeur critique de 2,776.
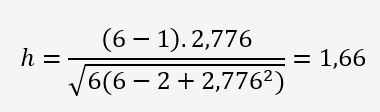
h est une tolérance bilatérale: ±h
Un troisième tableau en bas de page donne directement la valeur critique de h à partir de p=6: 1,66.
| p | 1 | 2 | 3 |
4 |
5 | 6 | 7 | 8 |
| h |
-1,19 | -1,19 | / | / | 0,70 | 0,91 | 0,91 | -0,14 |
| k | ±1,66 (pour une probabilité de 95%) | |||||||
A ce stade, aucun thermocouple ne pose problème.
Conclusion: les différents tests de Mandel (k: dispersion et h: moyenne) ont permis de détecter deux thermocouples (3 et 4) qui présente statistiquement une dérive, ils seront rebutés ou une valeur de correction leur sera attribuée si cela est possible.
9) Détection d'un éventuel biais commun:
Il s'agit de vérifier que les valeurs des différents thermocouples ne sont pas statistiquement différentes (ce qui ne devrait pas être le cas au regard des résultats).
Comme on dispose d'une valeur certifiée pour le thermocouple N°2, on connait la valeur de référence et l'incertitude associée.
On connait la moyenne et l'écart-type global en excluant les thermocouples N°3 et N°4.
On va déterminer l'écart-type de reproductibilité inter-équipement avec la formule:
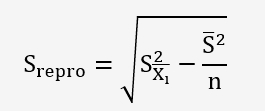
Sx
![]()
S² est la somme des carrés des écarts-types des moyennes/(p=6):
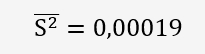
Et donc:
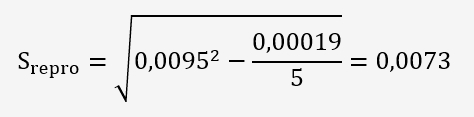
L'écart-type de la comparaison inter-équipement est donnée par la formule:
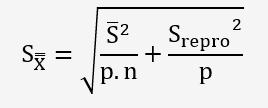
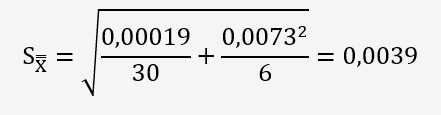
Déterminons enfin un Ecart normalisé pour vérifier que les valeurs ne sont pas différentes:
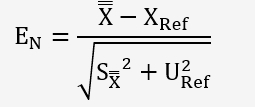
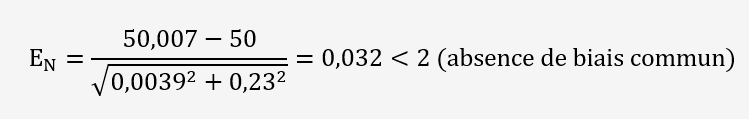
Table de Fischer-Snedecor
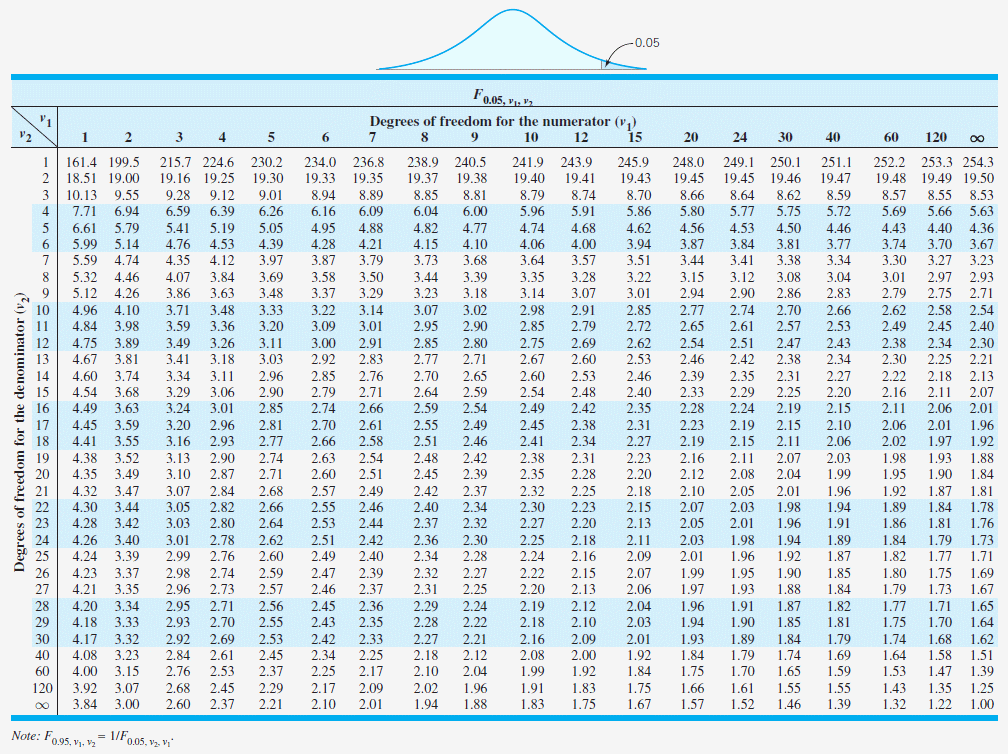
Table des valeurs critiques pour une distribution de student
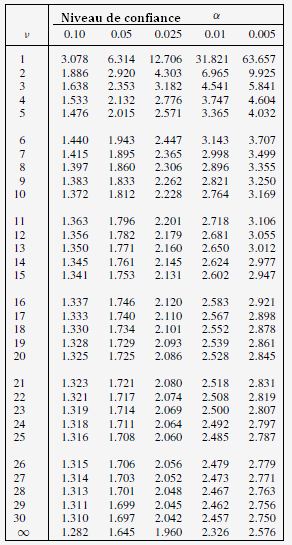
Table de Mandel h et k (Alpha=0,05)