La norme ISO/IEC 17025 impose de disposer d'un plan d'échantillonnage et d'une méthode d'échantillonnage.
Concernant la méthode, différents équipements permettent aujourd'hui de sécuriser une représentativité des échantillons, par contre si le plan d'échantillonnage doit se fonder sur des méthodes statistiques appropriées (§ 7.3.1), c'est plus difficile de l'établir en fonction des risques encourus par le demandeur (client) et le laboratoire.
Nous allons voir comment en fonction des risques, il est possible de définir un plan d'échantillonnage, qui devra toujours être en concertation avec le client.
L'objectif du laboratoire est d'optimiser les prélèvements afin de réduire les coûts associés et de ne pas y consacrer une période trop longue.
1) Quelques définitions:
- Niveau de qualité acceptable (NQA): le niveau de qualité souhaité par le client.
- Risque laboratoire (α): le risque que le plan d'échantillonnage ne parvienne pas à démontrer la qualité acceptable d'un lot et, donc, de le rejetez (erreur de type I), en général, ce risque est de 5%.
- Proportion de tolérance de lot défectueux (PTLD): le pire niveau de qualité que le client peut tolérer.
- Risque client (β): la probabilité d'accepter un lot avec un niveau de Qualité PTLD (erreur de type II), ce risque est généralement de 10%.
- Plan d'échantillonnage unique: une décision d'accepter ou de rejeter un lot basée sur les résultats d'un échantillon aléatoire du lot.
- Plan de double échantillonnage: un plan dans lequel on spécifie deux tailles d'échantillon et deux critères d'acceptation, si la qualité du lot est très bonne ou très mauvaise, le client peut décider d'accepter ou de refuser le lot sur la base du premier échantillon, qui est inférieur à celui du plan d'échantillonnage unique.
- Plan d'échantillonnage séquentiel: un plan dans lequel on sélectionne au hasard des articles du lot et on les contrôle un par un.
2) Plan d'échantillonnage unique:
La procédure consiste à prélever un échantillon aléatoire de taille (n) et à contrôler chaque élément.
Si le nombre de défauts ne dépasse pas un seuil d'acceptation spécifié (x), le client accepte l'ensemble du lot.
Tous les défauts trouvés dans l'échantillon sont soit réparés, soit renvoyés au fabricant.
Si le nombre de défauts dans l'échantillon est supérieur à (x), le client soumet l'ensemble du lot à un contrôle à 100 % ou rejette l'ensemble du lot et le renvoie au fabricant. Le plan d'échantillonnage unique est facile à utiliser mais se traduit généralement par un nombre d'objet à contrôler plus grand que les autres plans.
3) Plan de double échantillonnage:
Le laboratoire prend un échantillon aléatoire de taille n
Si le nombre de défauts est supérieur à (x
Si le nombre de défauts est compris entre (x
Un plan d'échantillonnage double peut réduire significativement
les coûts de contrôle par rapport à un plan d'échantillonnage
simple pour les lots à très faible ou très forte proportion
de défectueux car une décision peut être prise après
le premier prélèvement.
Cependant, si la décision nécessite deux échantillons,
les coûts d'échantillonnage peuvent être supérieurs
à ceux du plan d'échantillonnage unique.
4) Plan d'échantillonnage séquentiel:
Chaque fois qu'un article est contrôlé, une décision
est prise pour (1) rejeter le lot, (2) accepter le lot, ou (3) continuer l'échantillonnage,
sur la base des résultats cumulés jusqu'à présent.
Le laboratoire trace le nombre total d'articles défectueux par rapport
à la taille cumulée de l'échantillon, et si le nombre
de défectueux est inférieur à un critère d'acceptation
(x
Si le nombre est supérieur à un autre critère d'acceptation
(x
Si le nombre se situe quelque part entre les deux, un autre article est contrôlé.
Le nombre moyen d'articles contrôlés est généralement
plus faible pour le plan d'échantillonnage séquentiel que pour
toute autre forme d'échantillonnage, ce qui entraîne des coûts
moindres.
Pour des valeurs très faibles ou très élevées de la proportion de défectueux, l'échantillonnage séquentiel fournit un nombre moyen d'articles contrôlés inférieur à tout plan d'échantillonnage comparable.
Cependant, si la proportion d'unités défectueuses se situe entre le NQA et le PTLD, un plan d'échantillonnage séquentiel pourrait avoir un nombre moyen d'articles contrôlés plus grand qu'un plan d'échantillonnage simple ou double comparable (bien que cela soit peu probable).
En général, le plan d'échantillonnage séquentiel peut réduire le nombre moyen d'articles contrôlés à 50 % de celui requis par un plan d'échantillonnage unique comparable et, par conséquent, économiser des coûts de contrôle substantiels.
Courbes caractéristiques de fonctionnement:
Le laboratoire crée un affichage graphique de la performance d'un
plan d'échantillonnage en traçant la probabilité d'accepter
le lot pour une gamme de proportions d'articles défectueux.
Ce graphique, appelé courbe de caractéristique de fonctionnement
(CF), décrit dans quelle mesure un plan d'échantillonnage discrimine
entre bons et mauvais lots.
Sans aucun doute, chaque client veut un plan qui accepte les lots avec un niveau de qualité supérieur au NQA sur 100 % du temps et n'accepte pas les lots avec un niveau de qualité inférieur au NQA .
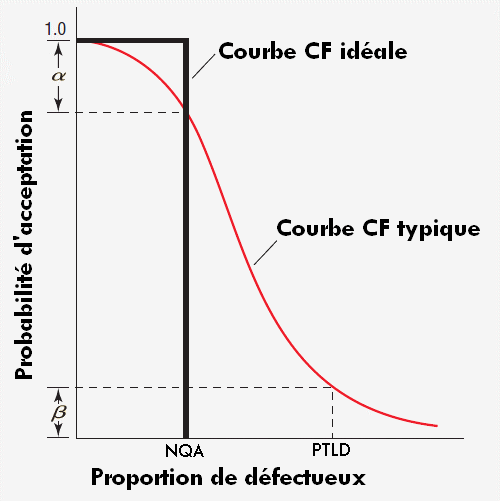
Cette courbe (CF) idéale pour un plan d'échantillonnage unique
est illustrée ci-dessous, cependant, de telles performances ne peuvent
être atteintes qu'avec un contrôle à 100 %.
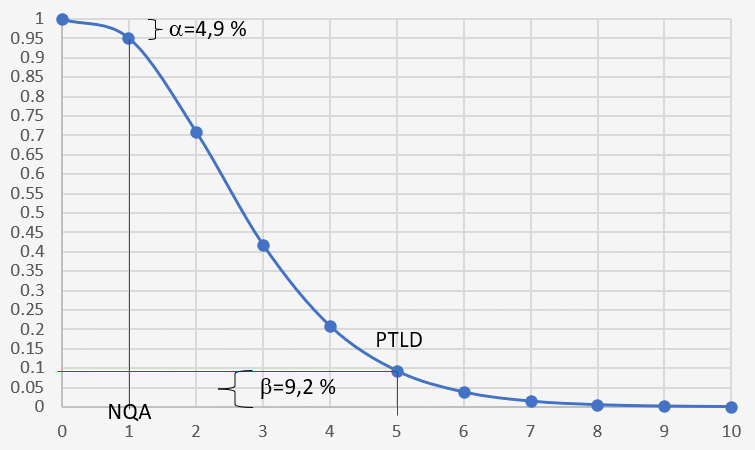
Une courbe (CF) typique pour un plan d'échantillonnage unique, tracée
en rouge, montre la probabilité α de rejeter un bon lot (risque
du laboratoire) et la probabilité β d'accepter un mauvais lot
(risque du client).
Par conséquent, le laboratoire devra choisir une taille d'échantillon n et le client un nombre de défauts autorisés: critères d'acceptation (x) pour atteindre le niveau de performance spécifié par le NQA, α, PTLD et β.
Déterminer la courbe CF:
La distribution d'échantillonnage pour le plan d'échantillonnage
unique est la distribution binomiale car chaque élément contrôlé
est soit défectueux (un échec), soit conforme (un succès).
La probabilité d'accepter le lot est égale à la probabilité
de prélever un échantillon de taille n dans un lot avec une
proportion de défectueux (p) et de trouver une quantité (x)
d'articles défectueux ou moins.
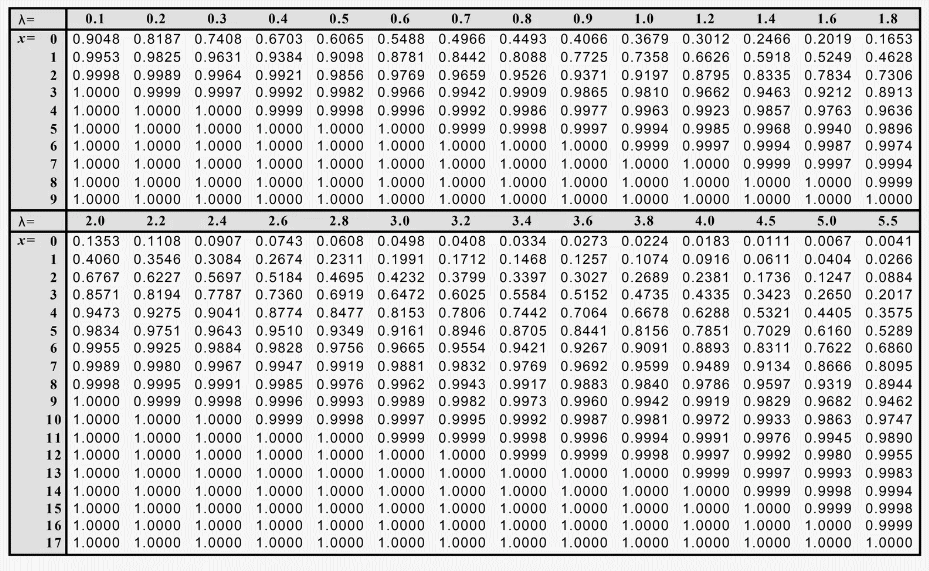
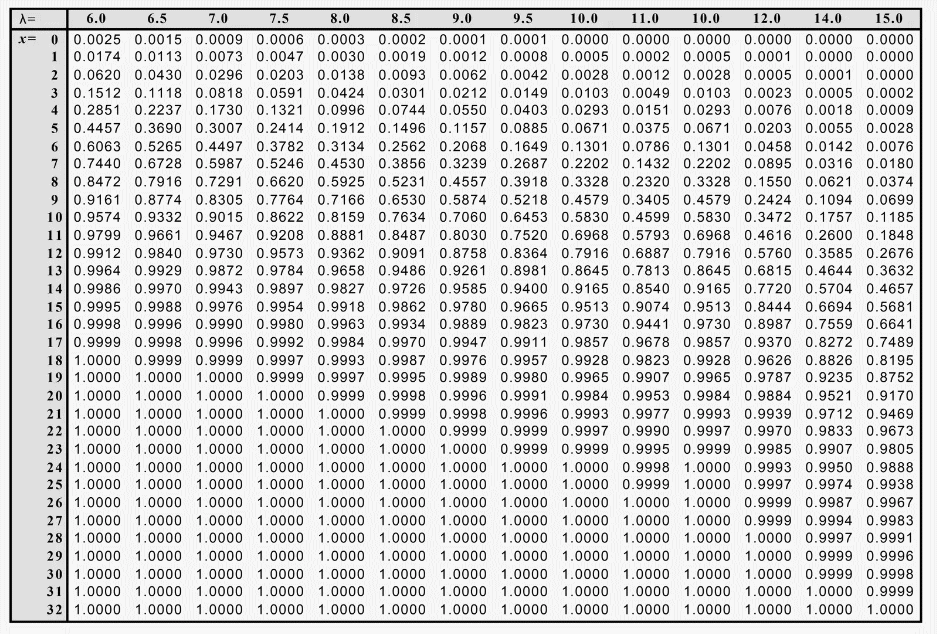
Cependant, si n est supérieur à 20 et (p) inférieur à 0,05 (5%), la distribution de Poisson peut être utilisée comme approximation du binôme pour tirer parti des calculs réalisés dans le but de tracer les courbes CF.
Pour tracer la courbe CF, recherchez la probabilité d'accepter le lot pour une plage de valeurs de (p).
Pour chaque valeur de (p),
1. Multiplier (p) par la taille de l'échantillon n.
2. Calculer la valeur de np.
3. Chercher dans la table la probabilité d'acceptation pour un critère
d'acceptation x et pour la valeur de np=λ.
4. Noter la valeur de la probabilité d'acceptation, P
Lorsque (p) = NQA, le risque du laboratoire α est égal à 1 moins la probabilité d'acceptation.
Lorsque (p) = PTLD, le risque du client β est égal à la probabilité d'acceptation.
Exemple concrêt de la détermination d'une courbe CF:
A la demande d'un client, un laboratoire doit contrôler à réception un lot de barres en acier inoxydable provenant d'un nouveau fournisseur, le lot fait 10 tonnes et comprend 435 barres de diamètre 25 mm.
Afin de ne pas contrôler toutes les barres, le laboratoire va échantillonner un nombre n de barre et analyser par fluorescence X un seul élément très caractéristique de l'alliage, le Niobium.
Le critère d'acceptation est x=1 (une seule barre non conforme autorisée)
Le contrat entre le client et le fournisseur stipule un NQA de 1% et un PTLD de 5%.
Le laboratoire décide de contrôler 25% des barres soit n=109.
| p | np=λ | P |
Calcul des risques |
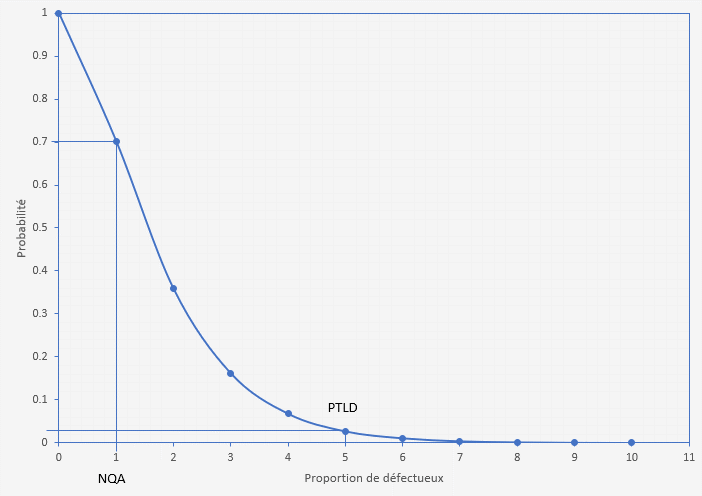
| 0,01 (NQA) | 1,09 | 0,702 | α=1,00-0,702=0,298 |
| 0,02 | 2,18 | 0,359 | |
| 0,03 | 3,27 | 0,162 | |
| 0,04 | 4,36 | 0,068 | |
| 0,05 (PTLD) | 5,45 | 0,027 | β=0,027 |
| 0,06 | 6,54 | 0,011 | |
| 0,07 | 7,63 | 0,004 | |
| 0,08 | 8,72 | 0,0016 | |
| 0,09 | 9,81 | 0,0006 | |
| 0,10 | 10,9 | 0,0002 |
Si la valeur de λ n'apparait pas dans la table ci-desous, vous pouvez utiliser EXCEL avec la fonction suivante:=LOI.POISSON.N(x;λ;Vrai)=LOI.POISSON.N(1;1,09;1)=0,702
On note que le risque du laboratoire est de 29,8% et le risque client dans la table est de 2,7%, le risque α est très supérieur au risque généralement acceptable de 5%.
Le laboratoire va devoir changer son plan d'échantillonnage pour réduire son risque.
Remarque:
- Pour un critère d'acceptation x constant, l'augmentation de la taille de l'échantillonnage n augmente le risque du laboratoire mais réduit le risque du client.
- Pour une valeur d'échantillonnage n constante, l'augmentation du critère d'acceptation x réduit le risque du laboratoire mais augmente le risque du client.
Le laboratoire et son client vont devoir faire des concessions.
Il existe des logiciels qui peuvent déterminer le couple (x,λ) optimal pour que les risques soient partagés et acceptables.
Une autre technique est de chercher le risque acceptable du client (10%) dans la table de poisson en augmentant le critère d'acceptation:
Par exemple, pour un λ=np=6,8 et un critère d'acceptation de 3, le risque du client est de 0,0928 soit 9,28%.
Pour un PTLD de 5%, la taille n de l'échantillonnage vaut: λ/p=6,8/0,05=136
Reprenons le tableau avec les nouvelles conditions:
Le critère d'acceptation du client est x=3
Le contrat entre le client et le fournisseur stipule un NQA de 1% et un PTLD de 5%.
Le laboratoire décide de contrôler n=136 barres soit 31% du lot.
| p | np=λ | P |
Calcul des risques |
| 0,01 (NQA) | 1,36 | 0,9506 | α=1,00-0,9506=0,049 |
| 0,02 | 2,72 | 0,7096 | |
| 0,03 | 4,08 | 0,4180 | |
| 0,04 | 5,44 | 0,2086 | |
| 0,05 (PTLD) | 6,8 | 0,0928 | β=0,0928 |
| 0,06 | 8,16 | 0,0380 | |
| 0,07 | 9,52 | 0,0146 | |
| 0,08 | 10,88 | 0,0053 | |
| 0,09 | 12,24 | 0,0002 | |
| 0,10 | 13,6 | 0,0006 |
On note que le risque du laboratoire est de 4,9% et le risque client est de 9,3%, les risques α et β sont respectivement inférieurs à 5 et 10% et sont donc considérés comme acceptables par les deux parties.
Vérification de la performance du plan:
Pour vérifier la performance du plan lorsque les contrôles ont été effectués, la laboratoire calculera la qualité sortante moyenne du plan (AOQ), qui est la proportion attendue de défauts maxi que le plan permettra de passer.
Nous supposons que toutes les barres non conformes du lot seront remplacées par de bonnes barres si le lot est rejeté et que toutes les barres non conformes du lot seront remplacées si le lot est accepté, cet état de fait se nomme "un programme de contrôle rectifié".
L'équation pour déterminée AOQ est:
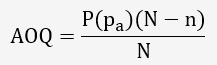
Avec P: proportion vraie de lot défectueux
Pa: Probabilité d'acceptation du lot
N: taille du lot = 435 barres
n: taille de l'échantillon = 136 barres
| p | np=λ | P |
P(P |
AOQ | AOQ % |
| 0,01 (NQA) | 1,36 | 0,9506 | 0,01.0,9506.(435-136) | 0,0065 | 0,65 |
| 0,02 | 2,72 | 0,7096 | 0,02.0,7096.(435-136) | 0,0097 | 0,97 |
| 0,03 | 4,08 | 0,4180 | 0,03.0,418.(435-136) | 0,0086 | 0,86 |
| 0,04 | 5,44 | 0,2086 | 0,04.0,2086.(435-136) | 0,0057 | 0,57 |
| 0,05 (PTLD) | 6,8 | 0,0928 | 0,05.0,0928.(435-136) | 0,0032 | 0,32 |
| 0,06 | 8,16 | 0,0380 | 0,06.0,038.(435-136) | 0,0016 | 0,16 |
| 0,07 | 9,52 | 0,0146 | 0,07.0,0146.(435-136) | 0,0007 | 0,07 |
| 0,08 | 10,88 | 0,0053 | 0,08.0,0053.(435-136) | 0,0003 | 0,03 |
| 0,09 | 12,24 | 0,0002 | 0,09.0,0002.(435-136) | 0,0001 | 0,01 |
| 0,10 | 13,6 | 0,0006 | 0,10.0,0006.(435-136) | 0 | 0 |
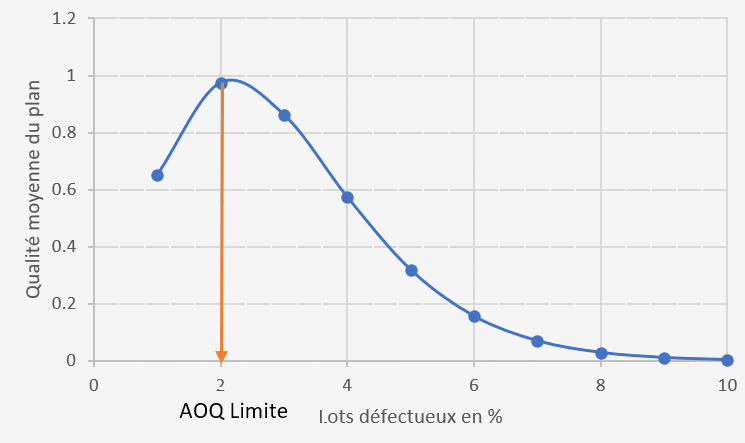
Le maximum de l'AOQ représente l'AOQ Limite et vaut 0,97%.
La probabilité correspondante en abcisse est de de 2% et représente le pire niveau de qualité résultant du programme de contrôle rectifié.
Ce niveau n'est pas très élevé, le plan d'échantillonnage corrigé est satisfaisant.
Table de Poisson des probabilités cumulatives