La norme ISO/IEC 17025 impose de participer à des essais d'aptitudes ou des essais interlaboratoires.
Malheureusement, toutes les méthodes d'essais ne font pas l'objet d'essais de comparaison disponibles et de surcroit, mis en œuvre pas un tiers accrédité ISO 17043 par un organisme notifié.
Dans ce cas, le laboratoire doit démontrer que les recherches effectuées n'ont pas permises d'identifier un organisme capable de proposer l'essai interlaboratoire concerné mais cela ne dédouane pas pour autant le laboratoire de répondre à l'exigence.
La laboratoire devra donc organiser lui-même un essais interlaboratoire avec d'autres laboratoires, la réalisation de cette comparaison peut être vue comme un échange de bon procédé et ne rien coûter ou presque pour chaque laboratoire impliqué ou bien entrainer des frais en sous-traitant l'essai concerné à d'autres laboratoires que l'on choisira sur la base de leur accréditation sur la méthode concernée.
Sur des essais très spécifiques, une recherche sur le territoire Français ne suffit pas, contacter le fournisseur du matériel et demandez-lui une liste de ces clients qui seraient potentiellement accrédités, à partir de ces informations, vous pouvez les contacter directement ou visiter le site internet des organismes notifiés (UKAS, A2LA, COFRAC; DAkkS;...) pour identifier précisément ceux avec qui, vous pourriez envisager de collaborer.
Il va donc falloir établir un protocole d'essai pour minimiser la dispersion de chaque participant et pour exploiter les données de sortie.
On considèrera que chaque laboratoire répond aux tests statistiques de GRUBBS et de COCHRAN: voir Fiche correspondante ICI.
1) Prenons un cas concret:
On suppose un laboratoire qui réalise des mesures de point de fusion par analyse thermique différentielle.
Ces mesures se font en laboratoire, il fait donc participer 4 autres laboratoires accrédités, qui vont chacun avec leur matériel faire 3 mesurages sur le même polymère, le laboratoire pilote se chargera d'exploiter l'ensemble des résultats qui seront transmis aux autres participants.
Les mesures sont exprimées en °C.
Les 5 laboratoires ont déterminés les résultats suivants:
| N° du Laboratoire | Résultats des 3 mesurages en °C | ||
| 1 | 131,1 | 130,4 | 130,3 |
| 2 | 130,9 | 129,8 | 129,9 |
| 3 | 131,0 | 129,8 | 130,5 |
| 4 | 129,9 | 130,0 | 129,8 |
| 5 (Pilote) | 130,1 | 130,7 | 130,2 |
Pour chaque laboratoire, le pilote va déterminer la moyenne, l'écartype de chaque laboratoire et l'écart-type moyen des écarts-types:
| N° du Laboratoire | Résultats des 3 mesurages | x̄ | s | ||
| 1 | 131,1 | 130,4 | 130,3 | 130,6 | 0,436 |
| 2 | 130,9 | 129,8 | 129,9 | 130,2 | 0,608 |
| 3 | 131,0 | 129,8 | 130,5 | 130,4 | 0,603 |
| 4 | 129,9 | 130,0 | 129,8 | 129,9 | 0,100 |
| 5 (Pilote) | 130,1 | 130,7 | 130,2 | 130,3 | 0,321 |
| Moyenne des moyennes: x̄ | 130,3 | ||||
| Ecart-type des moyennes:
s |
0,264 | ||||
| Moyenne quadratique
des écarts-types: s |
0,455 | ||||
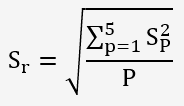
Il va ensuite déterminer la variance intralaboratoire:
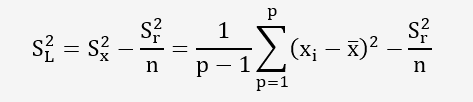
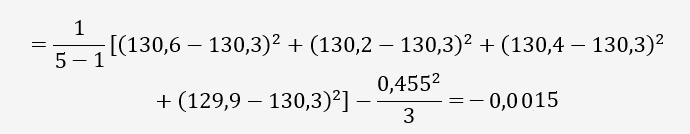
Note: Par convention, si S
Il va déterminer l'écart-type de reproductibilité inter-laboratoire:

On pourrait prendre l'écart normalisé pour comparer les résultats entre les différents laboratoires, mais ce critère est fortement tributaire de l'incertitude de chaque laboratoire, il suffit qu'un seul laboratoire ait une incertitude plus importante que les 4 autres pour que le critère EN < 2 soit respecté lors de la comparaison avec ce laboratoire et non respecté avec ceux ayant un incertitude plus petite.
Pour palier à ce défaut, nous allons utiliser les tests de Mandel k et h. Voir plus d'explication ICI.
Le pilote va déterminer la différence d de chaque laboratoire avec la moyenne générale:
| N° du Laboratoire | Résultats des 3 mesurages | d | ||
| 1 | 131,1 | 130,4 | 130,3 | 0,307 |
| 2 | 130,9 | 129,8 | 129,9 | -0,093 |
| 3 | 131,0 | 129,8 | 130,5 | 0,140 |
| 4 | 129,9 | 130,0 | 129,8 | -0,393 |
| 5 (Pilote) | 130,1 | 130,7 | 130,2 | 0,040 |
| Moyenne des moyennes: x̄ | 130,3 | |||
il va déterminer pour chaque laboratoire les statistiques de cohérence intra-laboratoire: k et inter-laboratoires: h
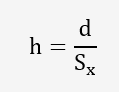 et
et
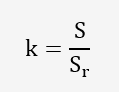
| N° du Laboratoire | Résultats des 3 mesurages | d | h | k | ||
| 1 | 131,1 | 130,4 | 130,3 | 0,307 | 1,16 | 0,96 |
| 2 | 130,9 | 129,8 | 129,9 | -0,093 | -0,35 | 1,34 |
| 3 | 131,0 | 129,8 | 130,5 | 0,140 | 0,53 | 1,32 |
| 4 | 129,9 | 130,0 | 129,8 | -0,393 | -1,49 | 0,22 |
| 5 (Pilote) | 130,1 | 130,7 | 130,2 | 0,040 | 0,15 | 0,71 |
| Ecart-type des moyennes:
s |
0,264 | |||||
| Ecart-type des écarts-types:
s |
0,455 | |||||
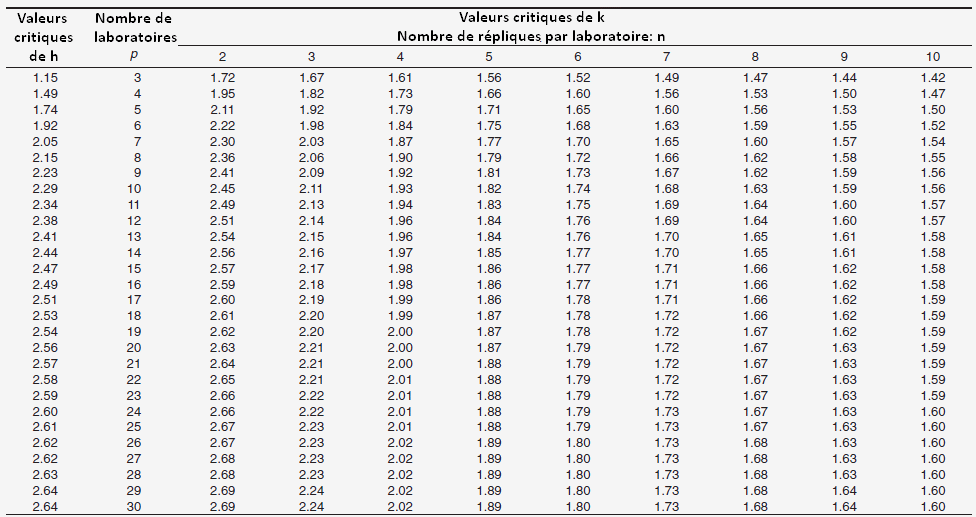
Pour p = 5 laboratoires et n = 3 répliques, la valeur critique de h est de ±1,74 et la valeur critique de k est de 1,92.
Aucune donnée n'est à l'extérieur des valeurs critiques, les résultats sont cohérents, le laboratoire pilote peut démontrer que le résultat de sa participation est satisfaisante.
Valeurs critiques de h et k à 0,5% de niveau de confiance