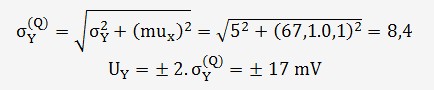Pente et incertitudes avec méthode des moindres carrés

Calculer une pente « m » et déterminer la valeur de l'ordonnée à l'origine « b » sont des opérations relativement simples.

Y = mx+b

Voici les étapes à suivre pour déterminer l'incertitude sur une valeur de Y en fonction de x, de la pente « m » et de l'ordonnée à l'origine « b ».

On considère un graphique (x,Y) constitué de N = 7 points distincts.

Prenons un exemple concrêt déjà traité (voir fiche Pente et incertitude): le titrage d'une solution lambda par un réactif, soit x le volume de titrant versé en ml et Y la réponse en mV de l'électrode.

On a obtenu les résultats suivants:

Données	Y	X
Unité	mV	ml
1	75	1,0
2	109	1,5
3	150	2,0
4	175	2,5
5	210	3,0
6	243	3,5
7	279	4,0

 

Détermination de la pente m et de la pente à l'origine b:

Pour ce faire, on va rechercher la meilleur droite en supposant que la variable x à une incertitude négligeable devant celle de Y et que l'incertitude de Y est la même pour chaque point de mesure et que les valeurs suivent une loi gaussienne (normale).

On va utiliser les équations "normales" pour déterminer b et m:

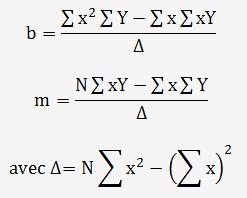
Déterminons les sous-calculs et les constantes:

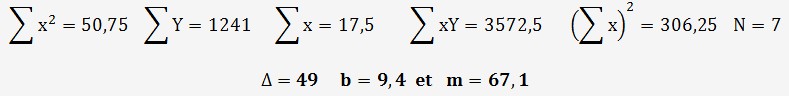
Nous allons estimer l'incertitude la plus vraissemblable en déterminant l'écart-type sur les valeurs de Y en considérant le degré de liberté sur une droite (N-2).

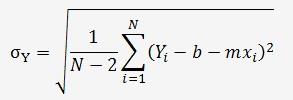
Bien sûr, il faut que N soit > 2.

Détermination de l'incertitude sur m et sur b:

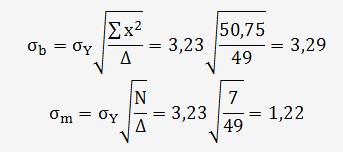
Cette incertitude ne prend pas en compte l'incertitude du Voltmètre ni celle sur le volume versé.

Si l'incertitude porte sur les valeurs de x et pas celles de Y, il suffit de permuter leur role respectif.

Il s'agit d'incertitude type qu'il faudra multiplier par un facteur d'élargissement k = 2.

Les valeurs peuvent sembler bien plus petites que la méthode graphique mais si l'on prend l'incertitude élargie sur x de l'exemple de la méthode graphique qui vaut ± 0,2 ml et que l'on détermine l'incertitude sur Y en tenant compte de l'incertitude sur Y = ± 10 mV.

On peut exprimer l'incertitude sur Y avec une moyenne quadratique, ce qui donne pour toutes valeurs de Y: